How We'll Begin Solving
The main challenge with traversing a BST in an inorder manner is keeping track of the ancestor. After all, at every node we visit, we will need to check if there is a node further on its left. This will need to continue until we reach a leaf node, i.e., node with no children as our starting point:
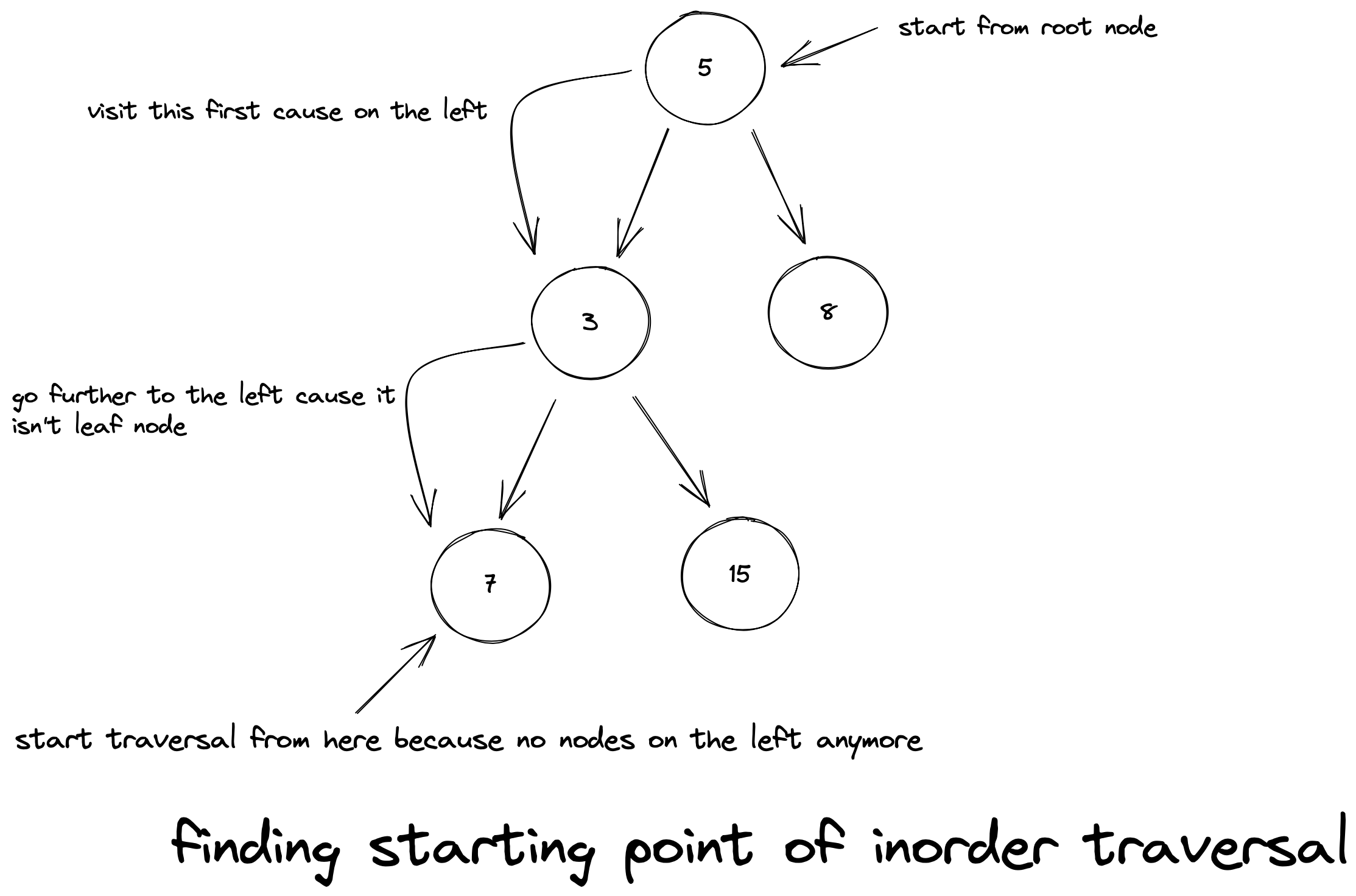
Once at a leaf node, we can start visiting the other nodes as per the traversal. We now understand the point of our two methods. isThereNextNode() has to be used to see if more nodes are yet to be visited in the traversal. It will be useful to stop the traversal if we have visited all of them. As long as there are more nodes to visit, nextNode() will have to keep track of them and visit them with each call.
One relatively naive approach is to use the stack data structure. Our constructor function can initialize the stack and keep track of the ancestors as it tries to find the leaf node to start with:
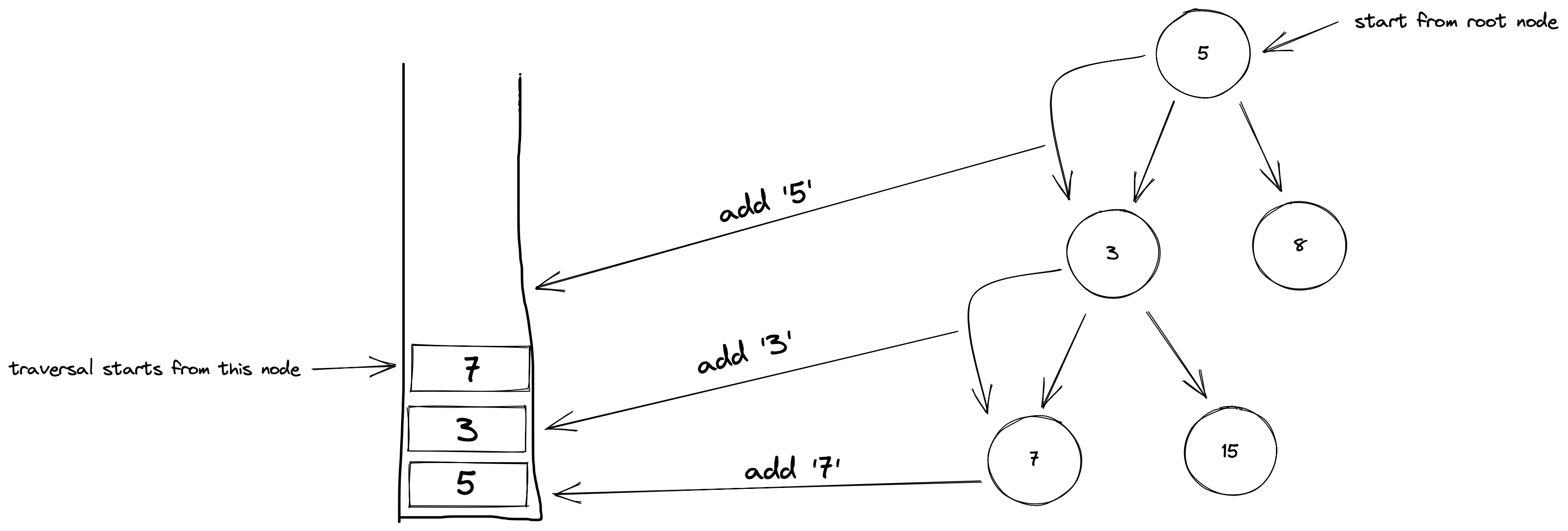
Then, we pop the stack and visit the node we get. We can check if the current node has a node to the right. If there is, we traverse it in an inorder way.
Have a look at the attached code that implements this approach.
xxxxxxxxxxconsole.log('traversalObj.isThereNextNode()', traversalObj.isThereNextNode());// Definition for a binary tree node.function TreeNode(val, leftNode, rightNode) { this.val = (val===undefined ? 0 : val) this.leftNode = (leftNode===undefined ? null : leftNode) this.rightNode = (leftNode===undefined ? null : rightNode)}class Stack { constructor() { this.items = []; } push(element) { this.items.push(element); } pop() { if (this.items.length == 0) return; return this.items.pop(); }}