Recall the definition of the Fibonacci numbers: they are a sequence of integers in which every number after the first two (0 and 1) is the sum of the two preceding numbers. To arrive at the sequence, we can quickly recognize there's a pattern in place, where we are repeating a similar calculation multiple times with different numbers.

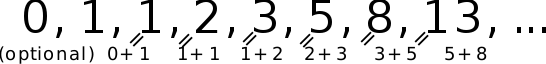
Time to reach into our toolbox-- this can readily be solved with recursion. At each recursive call, run the same calculation based off the same function for the prior elements. You can see the pseudo-code provided for how this can be accomplished.