This is an O(n^2) solution because it would require passing through each number, and then at each number scanning for a count.
A better way to do this is to take advantage of the property of a majority element that it consists of more than half of the set's elements.
What do I mean by this? Let's take another example, [4, 2, 2, 3, 2].
2 is obviously the majority element in the example from a visual scan, but how can we tip the algorithm off to this? Well, suppose we sorted the array:

[2, 2, 2, 3, 4]
Notice that if we hone in on index 2, that we see another 2. This is expected-- if we sort an array of numbers, the majority element will represent at least 50% of the elements, so it will always end up at the Math.floor(nums.length / 2)th index.
Depending on the sorting algorithm, this technique is usually O(n * log n) and requires either O(1) space if the sort is in-place, or O(n) space if not.
Another Method
Yet another way to solve this is to use the speed of a hash map! Hash maps allow access/look-ups in constant time, and its keys are guaranteed to be unique.
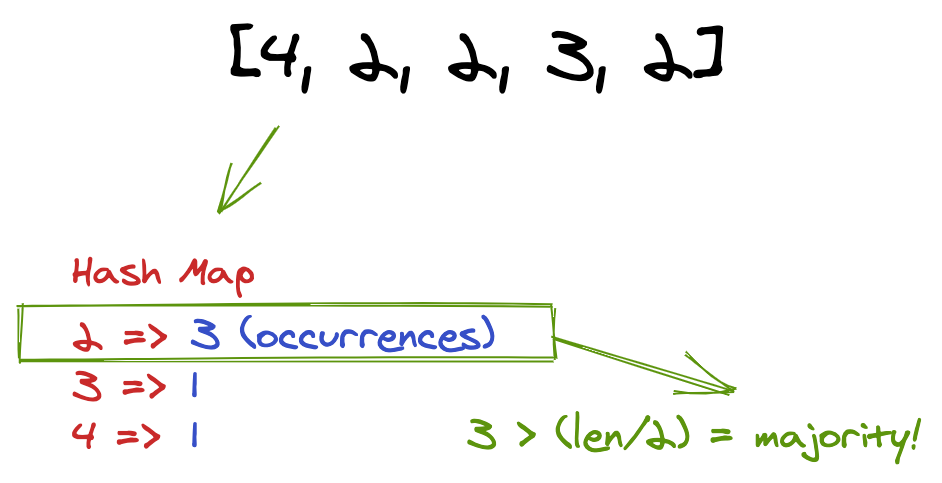
Thus, we can iterate through [2, 2, 2, 3, 4], and store each unique value as a key, and its attached value being the count. Each time we pass it, we increment its count, and use that information to relay we've got a current majority candidate.
1public class Main {
2 public static void main(String[] args) {
3 int[] nums = {4, 2, 2, 3, 2};
4 System.out.println(majorityElement(nums));
5 }
6
7 public static int majorityElement(int[] nums) {
8 HashMap<Integer, Integer> hash = new HashMap<>();
9 int max = 0;
10 int val = 0;
11
12 for (int i = 0; i < nums.length; i++) {
13 if (hash.containsKey(nums[i])) {
14 hash.put(nums[i], hash.get(nums[i]) + 1);
15 } else {
16 hash.put(nums[i], 1);
17 }
18
19 if (hash.get(nums[i]) > max) {
20 max = hash.get(nums[i]);
21 val = nums[i];
22 }
23 }
24 return val;
25 }
26}The time complexity of this solution is O(n) as it requires just one pass through the array, but has a space complexity of O(n) since it needs to maintain an auxiliary hash table.