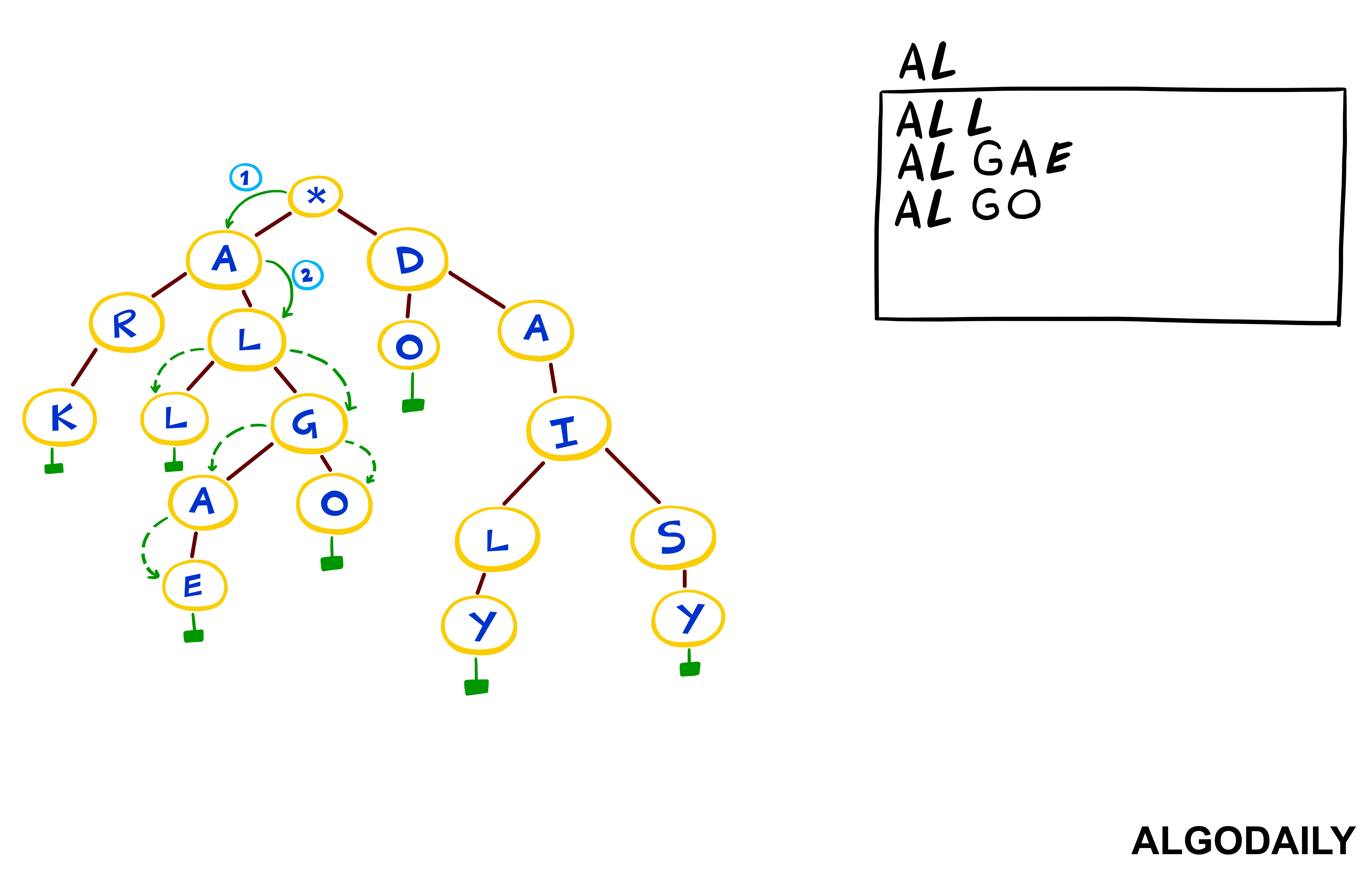
To implement a trie, we'll need to know the basics of how one works.

The easiest way is to imagine a tree in this shape:

1          *
2         / \ 
3        c   a
4       / \   \
5      a   o   end
6     / \   \
7    t   r   w
8   /     \   \
9  end    end  end

Next up, let's implement add.

A word is passed into the method (let's say "cat"), and begins to get processed. We'll first want to have references to the head node so that we can include each letter in cat as its eventual children and grandchildren. Here's how we accomplish establishing this lineage:

1Node currentNode = this.head;
2Node newNode = null;
3String currentChar = val.substring(0, 1);
4
5// val is used to keep track of the remaining letters
6val = val.substring(1);

We can use a while loop to determine the appropriate place to assign our word as a child key in a children hash. It does this by trying to look for each of our word's characters in the current node's children hash, and if there's a match, we try to place it in the next child's children hash. This handles the case where lineages like c -> a -> t in "category" may have already been previously added with a word like "cater".

1void add(String val) {
2  Node currentNode = this.head;
3  Node newNode = null;
4  String currentChar = val.substring(0, 1);
5  val = val.substring(1);
6
7  // See how deep we can get in any existing branches
8  while (
9    currentNode.children.get(currentChar) != null &&
10    currentChar.length() > 0
11  ) {
12    currentNode = currentNode.children.get(currentChar);
13    currentChar = val.substring(0, 1);
14    val = val.substring(1);
15  }
16}

Let's pause to ensure we've properly understood what's going on.

The prior code handled when there were children already registered. It doesn't make sense to add a new branch of c -> a if we encounter c -> a -> t, c -> a -> b, etc. So if we already have:

1  c
2 /
3a

and we're trying to add cat, we just add a new node for t at the end.

Next we'll use a while loop to iterate through each letter of the word, and create nodes for each of the children and attach them to the appropriate key. Depending on the language, there may be a more efficient implementation where the lookup and initialization happen simultaneously.

1void add(String val) {
2    TrieNode currentNode = this.getRoot();
3    TrieNode newNode;
4    String currentChar = val.substring(0, 1);
5    val = val.substring(1);
6
7    // See how deep we can get in any existing branches
8    while (
9            currentNode.getChildren().containsKey(currentChar) &&
10            currentChar.length() > 0
11    ) {
12        currentNode = currentNode.getChildren().get(currentChar);
13        currentChar = val.substring(0, 1);
14        val = val.substring(1);
15    }
16
17    // Break each character into levels respectively
18    // 'val' is the character, and 'value' lets us know if it terminates
19    while (currentChar.length() != 0) {
20        newNode = new TrieNode();
21        newNode.setVal(currentChar);
22        newNode.setValue(val.length() == 0 ? null : undefined);
23        newNode.setChildren(new HashMap<>());
24
25        currentNode.getChildren().put(currentChar, newNode);
26        currentNode = newNode;
27        currentChar = val.substring(0, 1);
28        val = val.substring(1);
29    }
30}

We can search the trie in O(n) time with n being the length of the word.

Finally, we can implement remove.

To know whether we should remove something, we should first check if the word is in the trie. So first, we'll need to do a search for it and see if we get a depth value returned.

1void remove(String val) {
2    int depth = this.search(val);
3    if(depth != 0) {
4        removeHelper(this.head, val, depth);
5    }
6}
7
8TrieNode remove(TrieNode root, String key, int depth) {
9    TrieNode pCrawl = root;
10
11    if (pCrawl == null)
12        return null;
13
14    if (depth == key.length()) {
15        if (pCrawl.isEndOfWord)
16            pCrawl.isEndOfWord = false;
17
18        if (isEmpty(pCrawl))
19            pCrawl = null;
20
21        return pCrawl;
22    }
23}

One Pager Cheat Sheet

• You should implement a Trie data structure with add, search, and remove methods that have O(n) time complexity & O(26 * n * N) space complexity, where n is the length of the word and N is the total number of strings.
• We need to be familiar with Tries, which can be represented by a tree structure like * / \ c a / \ o end / \ t r / \ end end end.
• Using add, search and remove, we can construct and utilize a class structure to create and traverse a tree structure, with a head node that branches off to each character value, and leaves to indicate the end of a word.
• Create references to the head node, then process each letter of the word (e.g. "cat") and add them as children or grandchildren, either adding a new key or marking the existing leaf node, depending on if the key is present or not.
• We can use a while loop to determine the appropriate place to assign our word as a child key in a children hash, searching for each of its characters and handling the lineages created by previously added words.
• Let's pause to ensure we've properly understood the situation, to avoid adding a new branch of c -> a when we already have c -> a -> t, c -> a -> b, etc.
• We can use a while loop to iterate through each letter of the word and create nodes and attach them to the appropriate key in both JS and Python.
• We can traverse from node to node to search for words by comparing our currentChar to the children's keys, and optionally returning the depth or the word itself once the end of the word is reached.
• We can search and remove words from the trie in O(n) time using removeHelper and _empty functions.
• We can recursively call a removeHelper method to delete any child nodes found.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx

}

import org.junit.Test;

import org.junit.runner.JUnitCore;

import org.junit.runner.Result;

import org.junit.runner.notification.Failure;

​

import static org.junit.Assert.*;

​

import java.util.HashMap;

​

class Trie {

    // fill in

    // with solution

    static class Node {

        public Character val;

        public boolean value;

        public HashMap<Character, Node> children;

​

        public Node(Character val) {

            this.val = val;

            this.value = false;

            this.children = new HashMap<Character, Node>();

        }

    }

​

    private Node head;

​

    public Trie() {

        this.head = new Node('\0');

    }

​

    public void add(String val) {

        Node currentNode = this.head;

Great job getting through this. Let's move on.

If you had any problems with this tutorial, check out the main forum thread here.