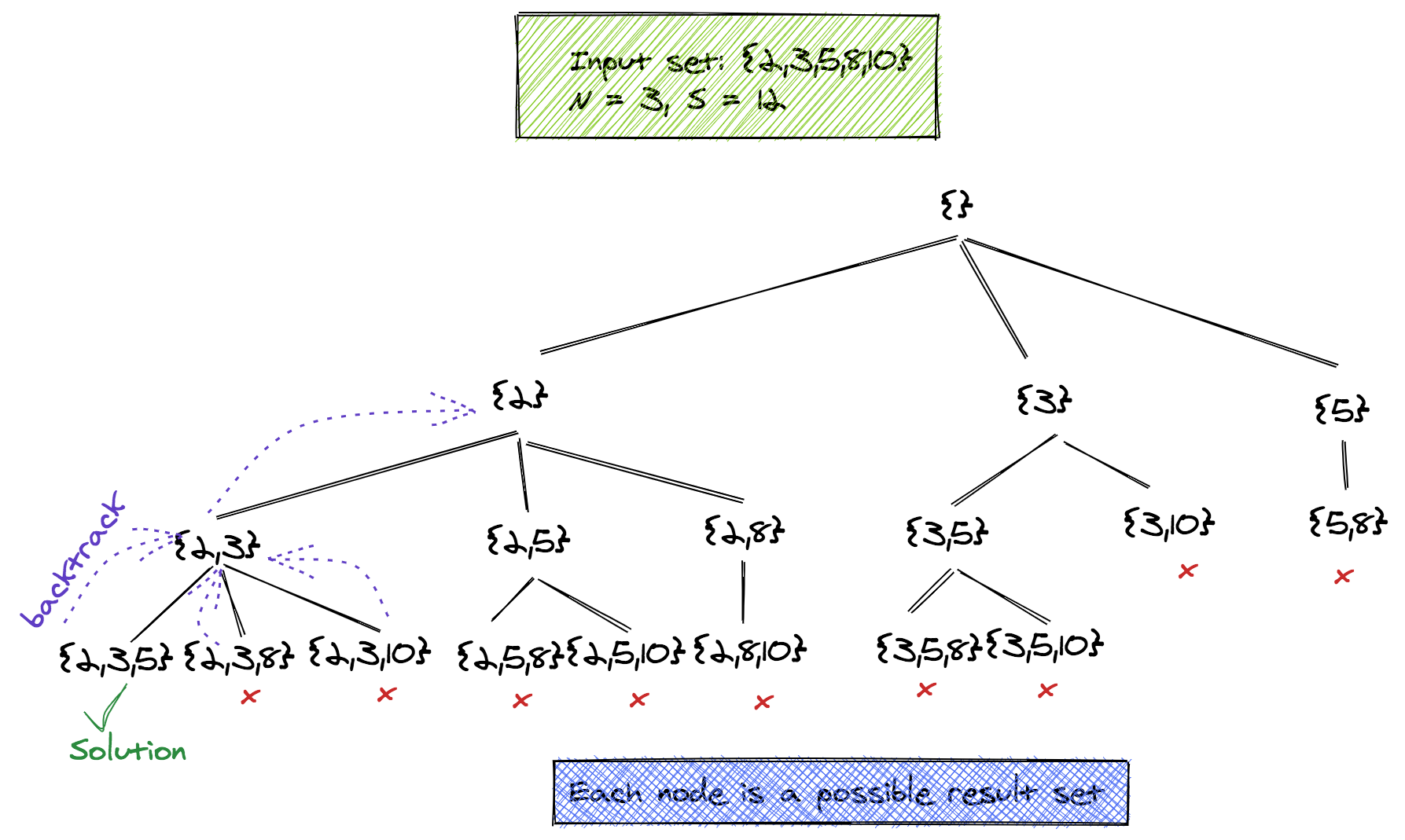
Combinatorial Problem With A Constraint: Finding N Combinations with Sum < S

Let's now add a constraint to our N combinations problem! The constraint is-- that all sets where sum < S (S being a given parameter) should be printed out.

All we need to do is modify the combosN code, so that all combinations whose sum exceeds S are not explored further, and other such combinations are not generated. Assuming the array is sorted, it becomes even more efficient.

We've illustrated backtracking via arrays to keep things simple. This technique would work really well for unordered linked lists, where random access to elements is not possible.

The tree below shows the abandoned paths {3, 10} and {5, 8}.

xxxxxxxxxx

// sum should be less than target of the argument.  Rest is the same as combosN function

void combosNConstraint(vector<int>& arr, vector<int>& subsets, int ind, int target)

{

    if (ind == arr.size())

        return;

    for (int i = ind; i < arr.size(); ++i) {

        subsets.push_back(arr[i]);

        // do a recursive call only if constraint is satisfied

        if (sum(subsets) <= target) {

            printVector(subsets);

            combosNConstraint(arr, subsets, i + 1, target);

        }

        subsets.pop_back();

    }

}