Create A Binary Search Tree Iterator

We know the binary search tree (BST) structure and the three ways to traverse it: inorder, preorder, and postorder. Now, let's create a class that takes a BST and can traverse it in an inorder fashion.

Prompt

Implement the BSTInorderTraversal class, whose each object acts as an iterator over the inorder traversal of a BST. The class will have a constructor and two methods to traverse a BST:

• BSTInorderTraversal (Node rootNode) initializes a class object. It takes a Node object called rootNode to traverse on. The iterating pointer should be initialized to some number lower than any element in the tree.
• int nextNode() moves to the next node in the traversal and returns the number at the node.
• boolean isThereNextNode() checks if there is a next node in the traversal to the right and returns True if there is and False if not.

Note how initializing the traversal pointer to a number lower than any element in the tree would ensure the first call to the nextNode() function returns the smallest element in the BST.

Once the class is created, you should be able to pass a BST and call the methods as the iterator would as it traverses.

Input: [[BSTInorderTraversal, ], 'nextNode', 'isThereNextNode', 'nextNode', 'nextNode', 'isThereNextNode', 'nextNode', 'nextNode', 'isThereNextNode'] //array of function calls

[[5,3,8,null,null,7,15],[],[],[],[],[],[],[],[]] //array of parameters

The first array represents all the function calls that will be made. The second array shows the parameters passed to each function in the respective order. See the Explanation section below.

Output: [null,3,5,7,8,15] // array of returned values

This array represents the values that will get returned in a particular order.

Explanation:

The object will be instantiated and the methods called in the following way: ``` Node root = Node(5); root.left = new Node(3); root.right = new Node(8); root.right->left = new Node(7); root.right->right = new Node(15);

BSTInorderTraversal traversalObj = new BSTInorderTraversal(root]); traversalObj.nextNode(); //should return 3 traversalObj.isThereNextNode(); //should return true traversalObj.nextNode(); //should return 5 traversalObj.nextNode(); //should return 7 traversalObj.isThereNextNode(); //should return true traversalObj.nextNode(); //should return 8 traversalObj.nextNode(); //should return 15 traversalObj.isThereNextNode(); //should return false ```

Constraints

• The number of nodes in the BST that would get traversed is in the range [1,10⁵].
• 0 <= Node.val <= 106
• The isThereNextNode, and nextNode will get called at most 105 times.
  

Before moving on to the solution, try out solving the problem yourself below. The window shows how the Node class is defined.

Let's Go Through The Solution

Before we move on to the problem's solution, let's check your prior knowledge and intuition.

Question 1: In what order does inorder traversal visit a tree's nodes? Option 1: [left node, right node, root]

Option 2: [root, left node, right node]

Option 3: [left node, root, right node]

Option 4: [right node, left node, root]

On Interviewer's Mindset

Tree traversal challenges are common in tech interviews, and BSTs are a particular favorite of interviewers. The special policy of BST makes related problems come with an inherent constraint. Combined with other constraints of a problem, BST-based problems can show how well an applicant understands trees and the efficient way of traversing them.

With a question like this, your programming skills are being tested. Since you have to define a class and its methods, you can use object-oriented programming to your advantage. Hence, make sure to understand this question and its solution thoroughly.

How We'll Begin Solving

The main challenge with traversing a BST in an inorder manner is keeping track of the ancestor. After all, at every node we visit, we will need to check if there is a node further on its left. This will need to continue until we reach a leaf node, i.e., node with no children as our starting point:

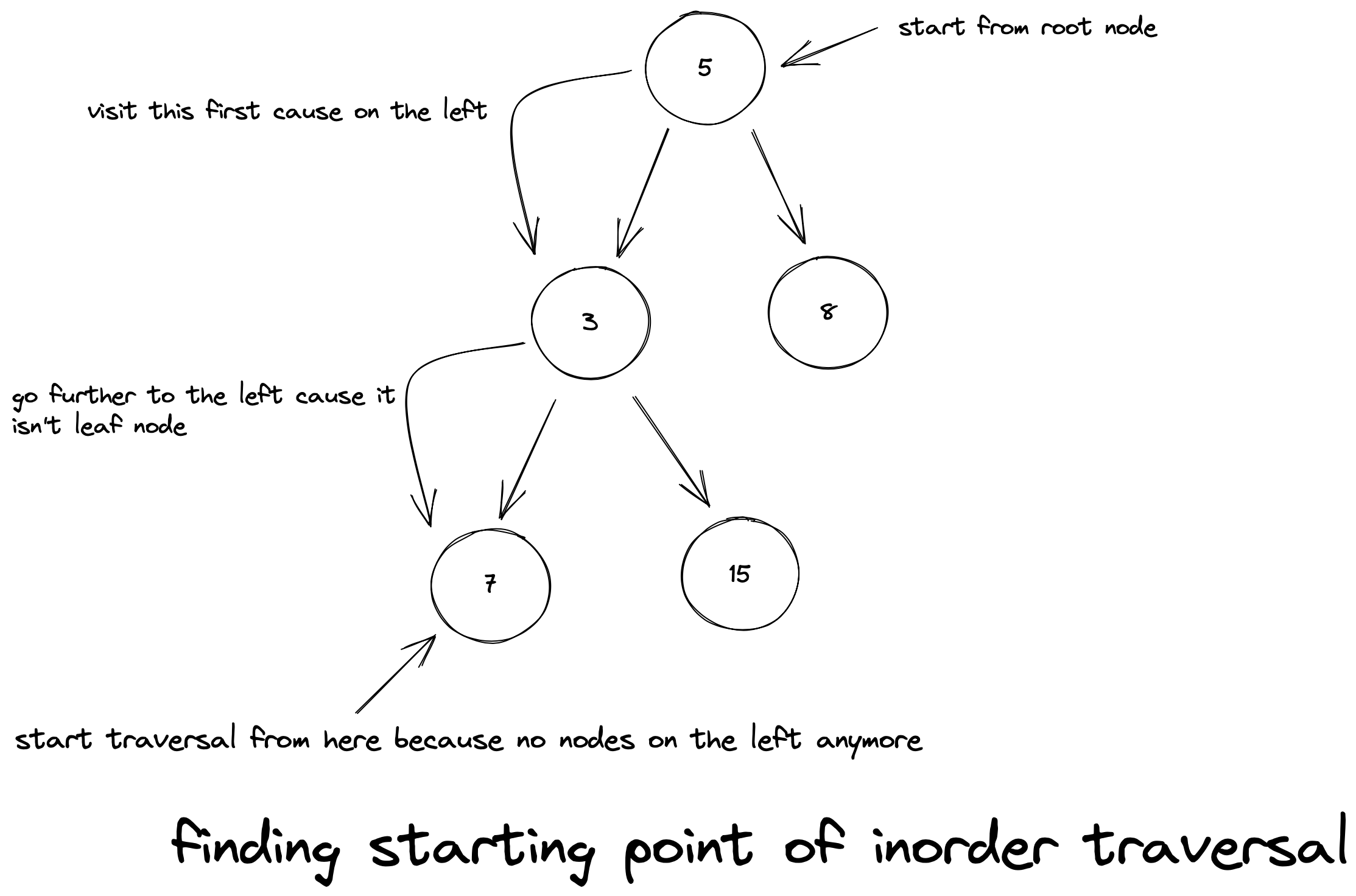
Once at a leaf node, we can start visiting the other nodes as per the traversal. We now understand the point of our two methods. isThereNextNode() has to be used to see if more nodes are yet to be visited in the traversal. It will be useful to stop the traversal if we have visited all of them. As long as there are more nodes to visit, nextNode() will have to keep track of them and visit them with each call.

One relatively naive approach is to use the stack data structure. Our constructor function can initialize the stack and keep track of the ancestors as it tries to find the leaf node to start with:

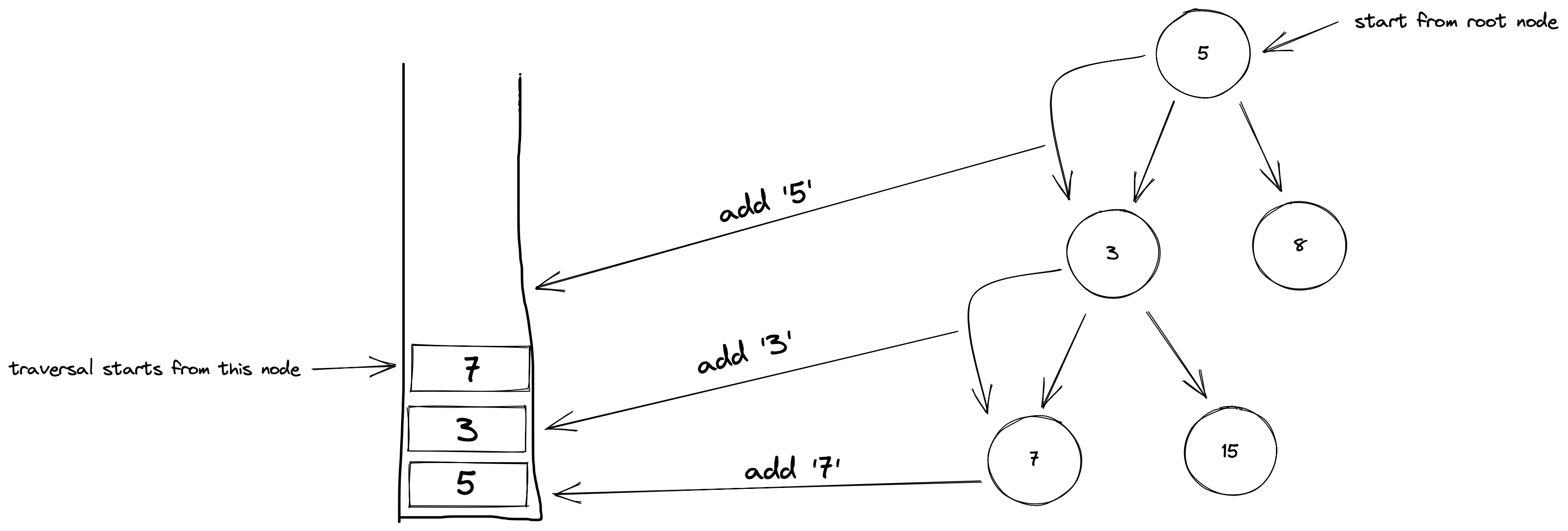
Then, we pop the stack and visit the node we get. We can check if the current node has a node to the right. If there is, we traverse it in an inorder way.

Have a look at the attached code that implements this approach.

```java
import java.util.Stack;
import java.util.NoSuchElementException;  

// solution

import java.util.ArrayList;

class BSTInorderTraversal {

    private Stack<Node> nodeStack;

    public BSTInorderTraversal(Node rootNode) {
        nodeStack = new Stack<Node>();
        Node currentNode = rootNode;

        while (currentNode != null) {
            nodeStack.push(currentNode);
            currentNode = currentNode.leftNode;
        }
    }

    public int nextNode() {
        if (!isThereNextNode())
            throw new NoSuchElementException();
 
        Node currentNode = nodeStack.pop();
        
        Node tempNode = currentNode.rightNode;
        if (tempNode != null)
            while (tempNode != null) {
                nodeStack.push(tempNode);
                tempNode = tempNode.leftNode;
            } 

        return currentNode.val;
    }

    public boolean isThereNextNode() {
        return !nodeStack.isEmpty();
    }

}

public class Main
{
	public static void main(String[] args) {
        Node tree1;

        tree1 = new Node(5);
        tree1.leftNode = new Node(3);
        tree1.rightNode = new Node(8);
        tree1.rightNode.leftNode = new Node(7);
        tree1.rightNode.rightNode = new Node(15);

        BSTInorderTraversal traversalObject1 = new BSTInorderTraversal(tree1);


        System.out.println("traversalObject1.nextNode() got");
        System.out.println(traversalObject1.nextNode());

        System.out.println("traversalObject1.isThereNextNode() got");
        System.out.println(traversalObject1.isThereNextNode());
	}
}

class Node {
    public int val;

    public Node leftNode;
    public Node rightNode;

    public Node(int val) {
        this.val = val;
    }
}
```
```js
// Definition for a binary tree node.
function TreeNode(val, leftNode, rightNode) {
    this.val = (val===undefined ? 0 : val)
    this.leftNode = (leftNode===undefined ? null : leftNode)
    this.rightNode = (leftNode===undefined ? null : rightNode)
}

class Stack {

	constructor()
	{
		this.items = [];
	}

    push(element)
    {
        this.items.push(element);
    }

    pop()
    {
        if (this.items.length == 0)
            return;
        return this.items.pop();
    }

}


/**
 * @param {TreeNode} rootNode
 */

var BSTInorderTraversal = function(rootNode) {
    this.nodeStack = new Stack();
    let current = rootNode;

    while (current != null) {
        this.nodeStack.push(current);
        current = current.leftNode;
    }

};

/**
 * @return {number}
 */
BSTInorderTraversal.prototype.nextNode = function() {
    if (!this.isThereNextNode())
        return;
    let current = this.nodeStack.pop();

    if (current.right != null)

        var temp = current.rightNode;
        while (temp != null) {
            this.nodeStack.push(temp);
            temp = current.leftNode;
    }

    return current.val;

};

/**
 * @return {boolean}
 */
BSTInorderTraversal.prototype.isThereNextNode = function() {
    if (this.nodeStack.items.length) {
        return true
    } else {
        return false
    }
};

let root = new TreeNode(5);
root.leftNode = new TreeNode(3);
root.rightNode = new TreeNode(8);
root.rightNode.leftNode = new TreeNode(7);
root.rightNode.rightNode = new TreeNode(15);

traversalObj = new BSTInorderTraversal(root);

console.log('traversalObj.nextNode() got', traversalObj.nextNode());
console.log('traversalObj.isThereNextNode()', traversalObj.isThereNextNode());
```
```py
# Definition for a binary tree node.
class Node:
    def __init__(self, val=0, leftNode=None, rightNode=None):
        self.val = val
        self.left = leftNode
        self.right = rightNode

class BSTInorderTraversal:
    nodeStack = []

    def __init__(self, root):
        current = root

        while current != None:
            self.nodeStack.append(current)
            current = current.left

    def isThereNextNode(self) -> bool:
        return False if len(self.nodeStack) == 0 else True 

    def nextNode(self) -> int:
        if (not self.isThereNextNode()):
            return
        
        current = self.nodeStack.pop()
        if (current.right != None):
            temp = current.right
            while temp != None:
                self.nodeStack.append(temp)
                temp = current.left

        return current.val

root = Node(5)
root.left = Node(3)
root.right = Node(8)
root.right.left = Node(7)
root.right.right = Node(15)

traversalObj = BSTInorderTraversal(root)

print('traversalObj.nextNode() gets', traversalObj.nextNode())
print('traversalObj.isThereNextNode()', traversalObj.isThereNextNode())
```

Is There A Better Solution?

While this solution was pretty straightforward, there is much room for improvement. The complexity of the above solution is O(N), where N is the number of nodes in the tree. Since it's a traversal challenge and we have to visit each node, this makes sense.

However, the space complexity here is also O(N) since the stack will eventually hold all nodes. If the tree has a long height, the stack could manage thousands of nodes simultaneously. Hence, we can try to improve this complexity.

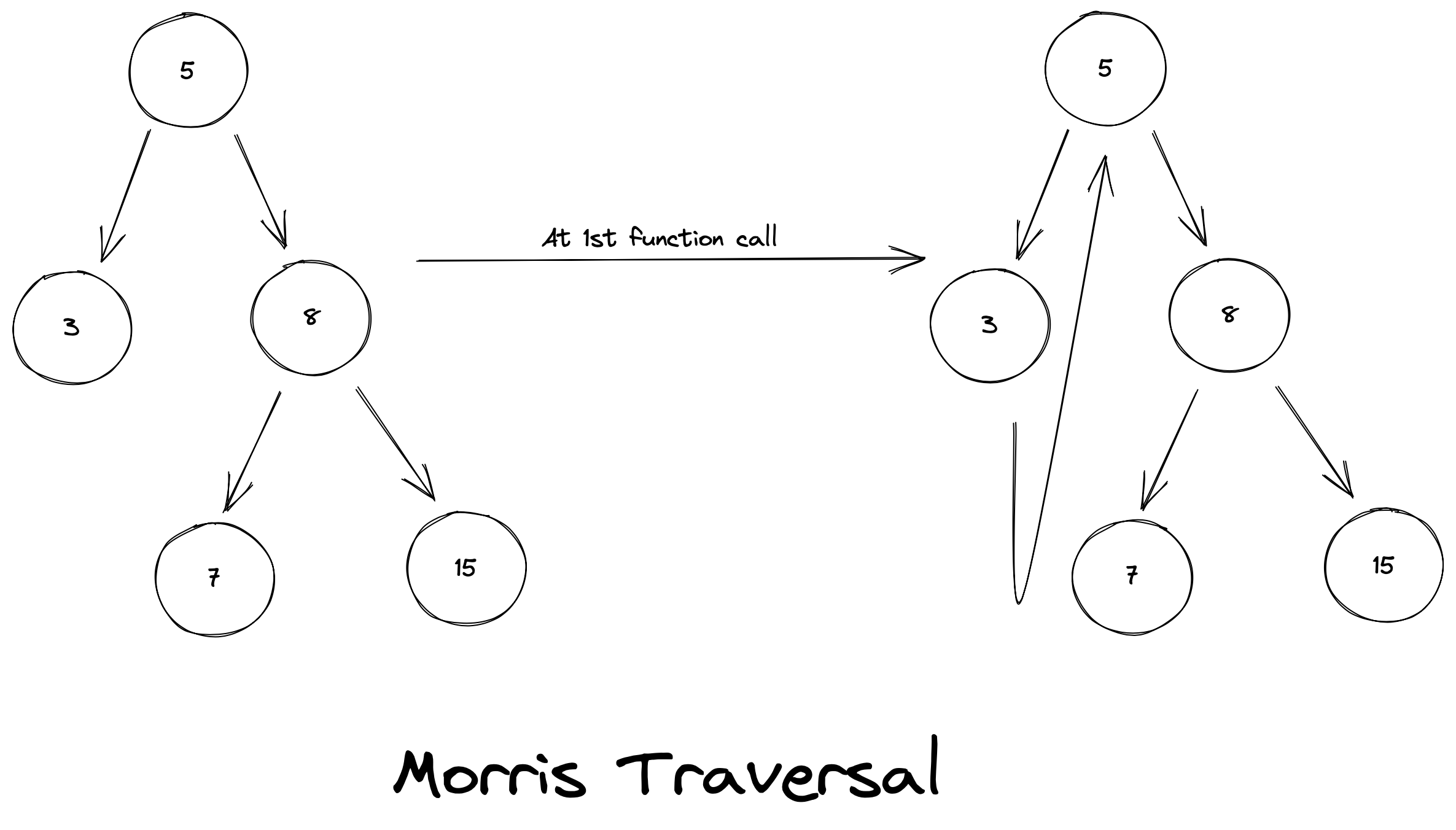
A better approach (called Morris Traveral) uses recursion to solve the problem efficiently. It also uses the fact that we can save references to nodes in the Node object's attributes: Node rightNode and Node leftNode as shown above.

When we start from a certain node A, we try to find the rightmost leaf node of its left and right subtrees. Once we reach this leaf node, we see its right node stores null. We can use this pointer to store the address of the ancestor node A:

Question 2

Given the following recursive function, will it iterate infinitely if we call recur(5)? py def recur(num): if num == 1: return num else: return recur(num-1)+recur(num-3)

This approach uses temporary objects and pointers that we use to hold references. These variables' values constantly get reassigned. Hence, the space complexity becomes constant!.

If you haven't by now, try solving the problem before viewing the final solution.

One Pager Cheat Sheet

• Create a BSTInorderTraversal class that implements an iterator that traverses a binary search tree (BST) in an inorder fashion.
• Inorder traversal visits the nodes of a tree in the order left node, root, right node in a recursive manner.
• Candidates should understand the BST-based problem and use object-oriented programming to their advantage when solving it.
• We can use a naive stack approach to traverse a binary search tree (BST) in an inorder manner, starting from a leaf node and visiting each ancestor while checking if there is a node to the right.
• We can improve the efficiency of the traversal challenge by using the Morris Traversal approach, which uses recursion and stores references to nodes in the Node objects's attributes, to avoids using extra memory and reduce time complexity.
• The function recur will infinitely recur since each time it is called it subtracts 3 from its argument so the base case of num==1 is never reached.
• The space complexity of this approach is constant as values of variables are constantly reassigned.