Good afternoon! Here's our prompt for today.

This was submitted by user Hackleman.

Determine how "out of order" a list is by writing a function that returns the number of inversions in that list.

Two elements of a list L, L[i] and L[j], form an inversion if L[i] < L[j] but i > j.

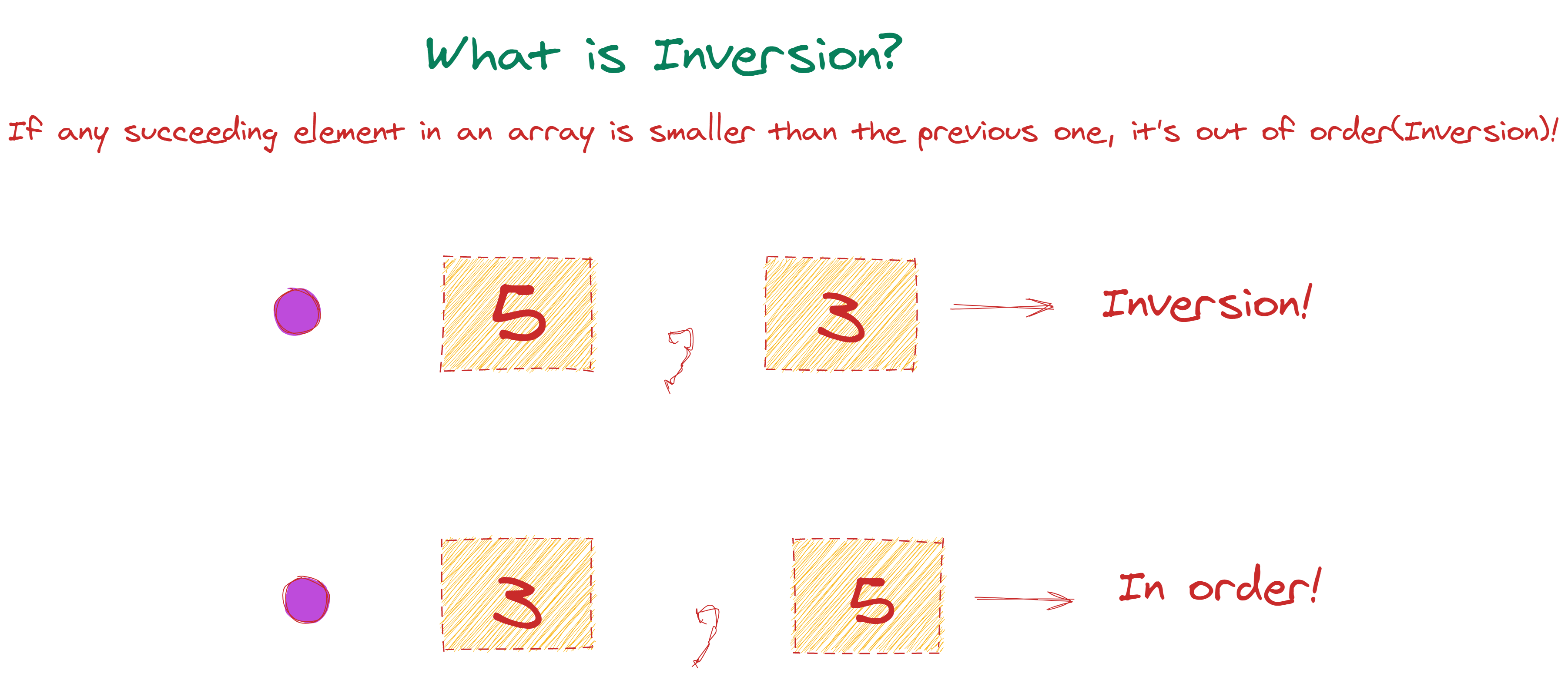
For example, the list [5, 4, 3, 2, 1] has 10 inversions since every element is out of order. They are the following: (5, 4), (5,3), (5,2), (5,1), (4,3), (4,2), (4,1), (3,2), (3,1), (2,1).

The list [2, 1, 4, 3, 5] has two inversions: (2, 1) and (4, 3).

Do this in better than O(N^2).

Constraints

• Length of the given array <= 100000
• Values in the array ranges from -1000000000 to 1000000000
• Expected time complexity : O(nlogn)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

var assert = require('assert');

​

// Please enter your coding solution here.

function inversions(list) {

  // fill in

  // return # of inversions

  return count;

}

// Though at AlgoDaily we have a strong bias towards Javascript,

// feel free to use any language you'd like!

​

try {

  assert.equal(inversions([5, 4, 3, 2, 1]), 10);

​

  console.log('PASSED: ' + 'inversions for [5, 4, 3, 2, 1] should be 10');

} catch (err) {

  console.log(err);

}

​

try {

  assert.equal(inversions([2, 4, 1, 3, 5]), 3);

​

  console.log('PASSED: ' + 'inversions for [2, 4, 1, 3, 5] should be 3');

} catch (err) {

  console.log(err);

}

​

try {

  assertIsFunction(inversions, '`inversions` should be a function');

Here's how we would solve this problem...

How do I use this guide?