AlgoDaily - Implement the Trie Data Structure

Good morning! Here's our prompt for today.

Suppose you're asked during an interview to design an autocompletion system. On the client side, you have an input box. When users start typing things into the input, it should parse what's been typed and make suggestions based on that.

For example, if the user has typed "cat", we may fetch "cat", "category", and "catnip" as recommendations to display. This seems pretty simple-- we could just do a scan of all the words that start with "cat" and retrieve them. You can do this by storing the words in an array and doing a binary search in O(log n) time complexity, with n being the number of words to search through.

But what if you have millions of words to retrieve and wanted to separate the search time from vocabulary size?

A trie (for data reTRIEval), or prefix tree, would be what you want. Let's implement one today.

We should implement:

An add method that can add words to the trie
A search method that returns the depth of a word
A remove method that removes the word

Constraints

Total number of characters (not total number of strings) to be inserted <= 100000
The characters will only comprise of lowercase alphabets
Expected time complexity for add, search and delete : O(n) n being the length of the word
Expected space complexity : O(26 * n * N) where N is number of strings

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
package main
​
import "fmt"
​
const (
  ALBHABET_SIZE = 26
)
​
type trieNode struct {
  childrens [ALBHABET_SIZE]*trieNode
  isWordEnd bool
}
​
type trie struct {
  root *trieNode
}
​
func NewTrie() *trie {
  return &trie{
    root: &trieNode{},
  }
}
​
func (t *trie) Add(word string) {
  // fill in this methode
}
​
func (t *trie) Search(word string) int {
  // fill in this methode

We'll now take you through what you need to know.

How do I use this guide?

To implement a trie, we'll need to know the basics of how one works.

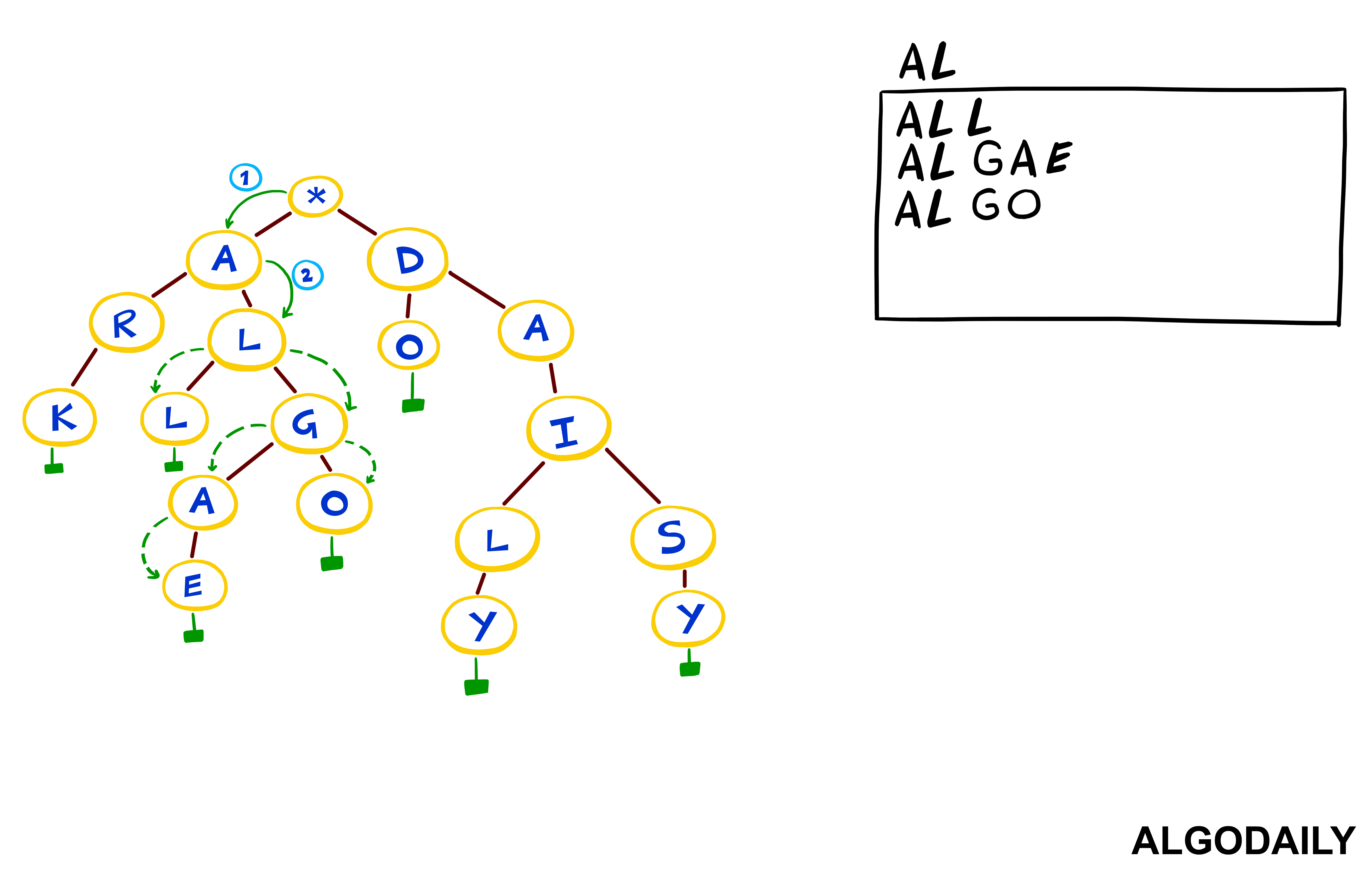
The easiest way is to imagine a tree in this shape:

SNIPPET

1          *
2         / \ 
3        c   a
4       / \   \
5      a   o   end
6     / \   \
7    t   r   w
8   /     \   \
9  end    end  end

Observing the above, you'll note that each path from the root to a leaf constitutes a string. Most nodes, except for the last, have a character value (except for the leaves which indicate the end, letting us know it's a word). So what we'd want to do in the following methods is:

add - create nodes and place them in the right place

search - traverse through nodes until you find possible words

remove - delete all associated nodes

Let's start by defining the class constructor. We'll start with just the head node, which will have a val property of an empty string (since it's only the root and can branch off to any letter), and an empty children object which we'll populate with add.

xxxxxxxxxx
 
type TrieNode struct {
  children [26]*TrieNode
  isEndOfWord bool
}
​
type Trie struct {
  root *TrieNode
}
​
func NewTrieNode() *TrieNode {
  node := &TrieNode{}
  node.isEndOfWord = false
  for i:=0; i<26; i++ {
    node.children[i] = nil
  }
  return node
}
​
func NewTrie() *Trie {
  trie := &Trie{}
  trie.root = NewTrieNode()
  return trie
}

Next up, let's implement add.

A word is passed into the method (let's say "cat"), and begins to get processed. We'll first want to have references to the head node so that we can include each letter in cat as its eventual children and grandchildren. Here's how we accomplish establishing this lineage:

1currentNode := this.head
2var newNode *Node = nil
3currentChar := val[0:1]
4
5// val is used to keep track of the remaining letters
6val = val[1:]

We can use a while loop to determine the appropriate place to assign our word as a child key in a children hash. It does this by trying to look for each of our word's characters in the current node's children hash, and if there's a match, we try to place it in the next child's children hash. This handles the case where lineages like c -> a -> t in "category" may have already been previously added with a word like "cater".

1func (t *Trie) Add(val string) {
2  currentNode := t.head
3  var newNode *Node
4  currentChar := string(val[0])
5  val = val[1:]
6
7  // See how deep we can get in any existing branches
8  for _, ok := currentNode.children[currentChar]; ok && len(currentChar) > 0; _, ok = currentNode.children[currentChar] {
9    currentNode = currentNode.children[currentChar]
10    currentChar = string(val[0])
11    val = val[1:]
12  }
13}

Let's pause to ensure we've properly understood what's going on.

The prior code handled when there were children already registered. It doesn't make sense to add a new branch of c -> a if we encounter c -> a -> t, c -> a -> b, etc. So if we already have:

SNIPPET

1  c
2 /
3a

and we're trying to add cat, we just add a new node for t at the end.

Next we'll use a while loop to iterate through each letter of the word, and create nodes for each of the children and attach them to the appropriate key. Depending on the language, there may be a more efficient implementation where the lookup and initialization happen simultaneously.

1func (t *trie) add(val string) {
2    currentNode := t.root
3    var newNode *node
4    currentChar := val[0:1]
5    val = val[1:]
6
7    // See how deep we can get in any existing branches
8    for currentNode.children[currentChar] != nil && len(currentChar) > 0 {
9        currentNode = currentNode.children[currentChar]
10        currentChar = val[0:1]
11        val = val[1:]
12    }
13
14    // Split each character into levels respectively
15    // 'val' is the character, and 'value' lets us know if it terminates
16    for len(currentChar) != 0 {
17        newNode = &node{
18            val: currentChar,
19            children: make(map[string]*node),
20        }
21
22        if len(val) == 0 {
23            newNode.value = nil
24        }
25
26        currentNode.children[currentChar] = newNode
27
28        currentNode = newNode
29        currentChar = val[0:1]
30        val = val[1:]
31    }
32}

We can move onto the search method!

This is similarly straightforward. The key part is again testing our currentChar/current character against the children hash's keys. If our current character is a child of the current node, then we can traverse to that child and see if the next letter matches as well.

Note that in our example, we're keeping track of depth and returning it. You can do this, or return the actual word itself once you hit the end of a word.

xxxxxxxxxx
}
 
package main
​
import (
  "fmt"
)
​
type TrieNode struct {
  Children [26]*TrieNode
  IsEndOfWord bool
}
​
type Trie struct {
  Root *TrieNode
}
​
func NewTrieNode() *TrieNode {
  node := &TrieNode{}
  for i := range node.Children {
    node.Children[i] = nil
  }
  node.IsEndOfWord = false
  return node
}
​
func CharToIndex(ch byte) int {
  return int(ch - 'a')
}
​
func (t *Trie) Add(key string) {

We can search the trie in O(n) time with n being the length of the word.

Finally, we can implement remove.

To know whether we should remove something, we should first check if the word is in the trie. So first, we'll need to do a search for it and see if we get a depth value returned.

1func (t *Trie) remove(val string) {
2    depth := t.search(val)
3    if depth != 0 {
4        t.removeHelper(t.head, val, depth)
5    }
6}
7
8func (t *Trie) remove(root *TrieNode, key string, depth int) *TrieNode {
9    pCrawl := root
10
11    if pCrawl == nil {
12        return nil
13    }
14
15    if depth == len(key) {
16        if pCrawl.isEndOfWord {
17            pCrawl.isEndOfWord = false
18        }
19        if empty(pCrawl) {
20            pCrawl = nil
21        }
22        return pCrawl
23    }
24    return nil
25}

If so, we can recursively call a removeHelper method to recursively delete child nodes if found.

xxxxxxxxxx
 
func removeHelper(node *Node, val string, depth int) bool {
    if depth == 0 && len(node.children) == 0 {
        return true
    }
​
    currentChar := string(val[0])
​
    if removeHelper(node.children[currentChar], val[1:], depth - 1) {
        delete(node.children,currentChar)
        if len(node.children) == 0 {
           return true
        } else {
           return false
        }
    } else {
        return false
    }
}

One Pager Cheat Sheet

You should implement a Trie data structure with add, search, and remove methods that have O(n) time complexity & O(26 * n * N) space complexity, where n is the length of the word and N is the total number of strings.
We need to be familiar with Tries, which can be represented by a tree structure like * / \ c a / \ o end / \ t r / \ end end end.
Using add, search and remove, we can construct and utilize a class structure to create and traverse a tree structure, with a head node that branches off to each character value, and leaves to indicate the end of a word.
Create references to the head node, then process each letter of the word (e.g. "cat") and add them as children or grandchildren, either adding a new key or marking the existing leaf node, depending on if the key is present or not.
We can use a while loop to determine the appropriate place to assign our word as a child key in a children hash, searching for each of its characters and handling the lineages created by previously added words.
Let's pause to ensure we've properly understood the situation, to avoid adding a new branch of c -> a when we already have c -> a -> t, c -> a -> b, etc.
We can use a while loop to iterate through each letter of the word and create nodes and attach them to the appropriate key in both JS and Python.
We can traverse from node to node to search for words by comparing our currentChar to the children's keys, and optionally returning the depth or the word itself once the end of the word is reached.
We can search and remove words from the trie in O(n) time using removeHelper and _empty functions.
We can recursively call a removeHelper method to delete any child nodes found.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
package main
​
import "fmt"
​
const (
  ALBHABET_SIZE = 26
)
​
type trieNode struct {
  childrens [ALBHABET_SIZE]*trieNode
  isWordEnd bool
}
​
type trie struct {
  root *trieNode
}
​
func NewTrie() *trie {
  return &trie{
    root: &trieNode{},
  }
}
​
func (t *trie) Add(word string) {
  wordLength := len(word)
  current := t.root
  for i := 0; i < wordLength; i++ {
    index := word[i] - 'a'
    if current.childrens[index] == nil {
      current.childrens[index] = &trieNode{}
    }
    current = current.childrens[index]

Alright, well done! Try another walk-through.

If you had any problems with this tutorial, check out the main forum thread here.