Good evening! Here's our prompt for today.
The Challenge: Unique Array Elements
You are given a sorted array of integers, named num. This array is special because it's sorted in non-decreasing order, meaning the numbers either stay the same or increase as you move through the array. However, there's a catch: the array might have duplicates, and your job is to make each number unique.
Example Scenarios
First Scenario:
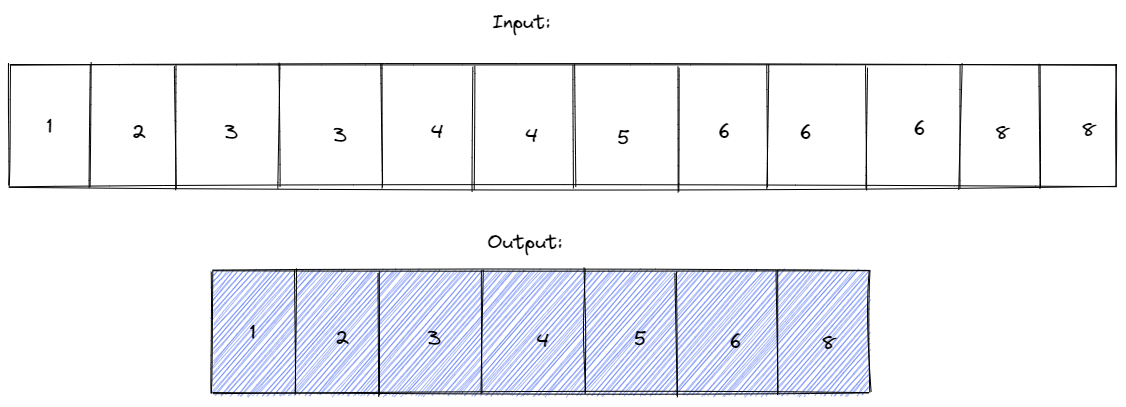
- Original Array:
num = [1, 2, 3, 3, 4, 4, 5, 6, 6, 6, 8, 8] - Expected Outcome:
- Length of Resultant Array: 8
- Resultant Array:
[1, 2, 3, 4, 5, 6, 8]
- Original Array:
Second Scenario:
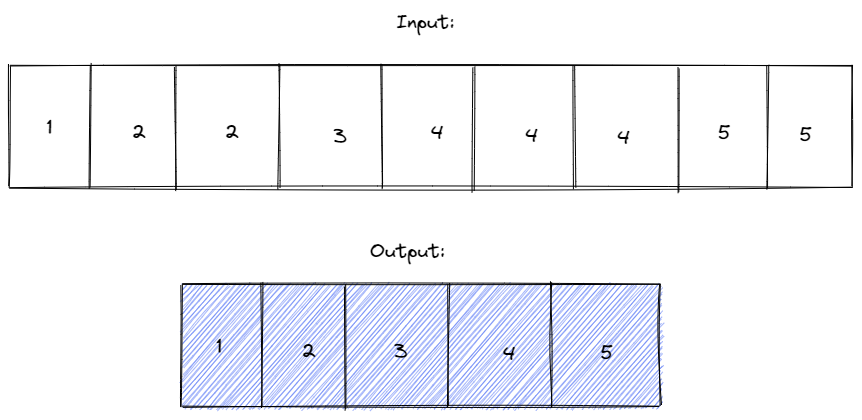
- Original Array:
num = [1, 2, 2, 3, 4, 4, 4, 5, 5] - Expected Outcome:
- Length of Resultant Array: 5
- Resultant Array:
[1, 2, 3, 4, 5]
- Original Array:
Your Objective
Develop a program that takes this sorted array and eliminates any duplicate elements. The challenge is to do this while maintaining the original order of the elements.
Key Constraints
- The input array,
num, is sorted in a non-decreasing manner. - The length of
numis always greater than 0.
Your task is to return two things: the length of the new array and the array itself, now with unique elements. This problem is a great way to understand array manipulation and the importance of maintaining order in data structures.
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxclass Twopointer(object): def RemoveDuplicates(self, nums, N): # Write your own code return lstdef test(): ob1 = Twopointer() nums1 = [2,3,4,4,5,6,6,6,7,8,8] nums2 = [1,1,2,3,4,4,5,6,6,7,8,9,9] nums3 = [2,4,4,6,8,10,10] assert ob1.RemoveDuplicates(nums1,len(nums1)) == [2, 3, 4, 5, 6, 7, 8],"Testcase passed" assert ob1.RemoveDuplicates(nums2,len(nums2)) == [1, 2, 3, 4, 5, 6, 7, 8, 9],"Testcase passed" assert ob1.RemoveDuplicates(nums3,len(nums3)) == [2,4,6,8,10],"Testcase passed"if __name__ == "__main__": test() print("Everything passed")Here's how we would solve this problem...
How do I use this guide?
Try this exercise. Click the correct answer from the options.
What would be the output for this array [1,2,2,3,6,6,9,10,10] after removing the duplicates? Click the option that best answers the question.
A. [1, 2, 4, 6, 10, 9]
B. [1, 2, 3, 6, 9, 10]
C. [1, 3, 4, 6, 10, 9]
D. [1, 2, 4, 6, 9, 10]
Click the option that best answers the question.
- A
- B
- C
- D
Disclaimer:
We have a very similar problem that we recently covered, called the Uniqueness of an Array. It is advisable not to mix it up with our current problem as the former one is removing duplicate elements from an unsorted array. In our case, we have a sorted array and therefore, allows us to use the two-pointers approach for an optimized solution. Let's look at the trivial brute force approach first before exploring the optimized solution.
Approaches:
Let's examine the two approaches and strategies and determine which is more efficient and optimized. Our first approach is brute force.
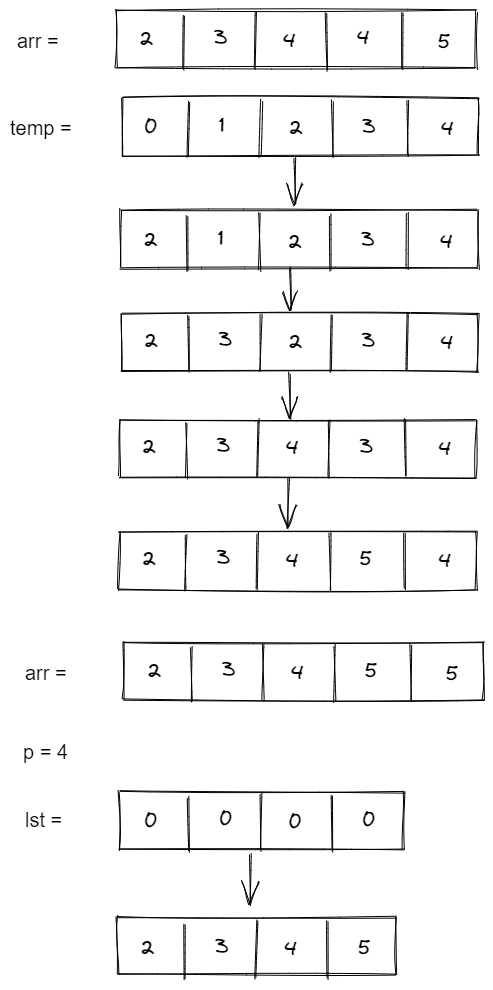
Brute Force Approach:
To identify and eliminate duplicates simultaneously, we may generate a new array that is the exact length of the original array and compare each element to its neighbor. In the case of a successful comparison, we would transfer one instance of the matching value from the original to the new array.
Solution Steps:
- Return the array by checking if the array's length is
0or1. - Declare a variable
tempto store the single instance of each element. - The input array will be scanned and copied a single instance of each element from
arrtotemp. - The variable
pwill be tracking the count of the single instance of each element. - We will copy each element's single instance from
temptoarr. - And last, we will return the length of the array and the resultant
arrby eliminating the duplicated element.
Here's to reference code for a better understanding!
1def RemoveDuplicates(arr, N):
2 if N == 0 or N == 1:
3 return N
4
5 temp = list(range(N))
6 p = 0;
7
8 for i in range(0, N-1):
9
10 if arr[i] != arr[i+1]:
11 temp[p] = arr[i]
12 p += 1
13
14 temp[p] = arr[N-1]
15 p += 1
16
17 for i in range(0, p):
18 arr[i] = temp[i]
19
20 return p
21
22arr = [2,3,4,4,5,6,6,6,7,8,8]
23a = len(arr)
24
25a = RemoveDuplicates(arr, a)
26print(a)
27lst =[]
28lst =[0 for i in range(a)]
29for i in range(a):
30 lst[i] = arr[i]
31print(lst)Build your intuition. Click the correct answer from the options.
What is the Space complexity of brute force?
Click the option that best answers the question.
- O(n)
- O(n!)
- O(nlogn)
- O(1)
Time Complexity:
The brute force approach has an O(n) time complexity, where n is the array's length. Moreover, the space complexity of the brute force approach is O(n) because a new array will be created, which will have the same length just like the original array.
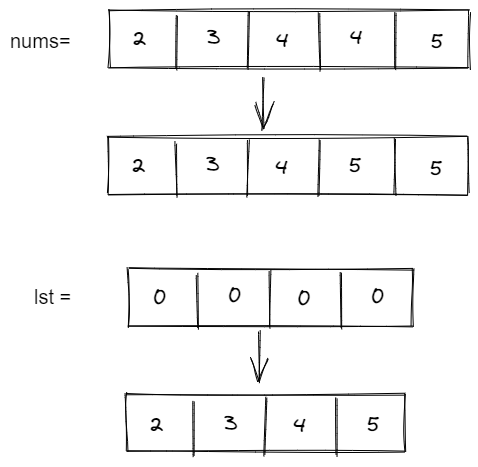
Two Pointers Approach:
As we know that the given array is sorted in non-decreasing order, we can have two pointers, i and j, where i and j represent slow-runner and fast-runner, respectively. On the condition that nums[i] = num[j], j is incremented to skip duplicates. If we find that nums[i]!=nums[j] then we will conclude the duplicate run and its value must be copied to nums[i + 1]. we will then increase the i, and the process is repeated until j arrives at the end of the array.
Solution steps:
- Initializing slow-runner and fast-runner variables
iandj, respectively. - The input array will be scanned till
j< lengthofnums. - We will identify a duplicate element by using this condition,
nums[i]==nums[j]; if the above condition matches, then we will skip the duplicate element, andjwill be incremented by1. Likewise, we will identify the unique element using this condition,nums[i]!=nums[j], if the above condition matches, theniwill be incremented by1. - Lastly, we will copy
nums[j]tonums[i]and increasejby1. - We will repeat the above steps till
jarrives at the end of the array, and the resultant output would bei+1and the resultant array by eliminating the duplicated element.
Try this exercise. Click the correct answer from the options.
What is the Space complexity of Two pointer Approach?
Click the option that best answers the question.
- O(n)
- O(n!)
- O(nlogn)
- O(1)
Time Complexity:
The above approach has a time complexity of O(n), where n represents the number of array elements. We only need to traverse the complete array once to identify the unique element. Additionally, the space complexity of the preceding method is O(1), as no additional space is required to eliminate duplicates from the sorted array.
Now its time to try and play around with the final solution!
One Pager Cheat Sheet
- We can develop a program to remove duplicate elements from a sorted array and return the length of the array, as well as the resultant array containing single instances of each element present.
- By comparing elements at consecutive indices, the output of the array
[1,2,2,3,6,6,9,10,10]after removing duplicates is[1, 2, 3, 6, 9, 10]. - Bringing an optimized solution to the problem of removing duplicates from a
sorted arrayusing atwo-pointersapproach, after discussing the slowerbrute forceapproach. Brute Forceis the more efficient and optimized approach to the two discussed strategies.- The brute force approach to removing duplicates from a sorted array involves iterating through the array, copying one instance of each value from the original array to a temporary array, and then copying each single instance from the temporary array to the original array.
- The total space complexity of the brute force approach is O(n), requiring
additional memoryequal to the size of the input arrayarr. - The brute force approach has an
O(n)time and space complexity, wherenis the array's length. - Using the two pointers approach, we can scan the given sorted array, identify duplicates and unique elements, and copy the unique elements to replace duplicates, in order to have a filtered array without duplicates.
- This approach has a Space complexity of
O(n)as it only utilizes two pointers,iandj. - The time complexity of this approach is
O(n), wherenis the number of elements in the array, and the space complexity isO(1)as no additional memory is required.
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxxclass Twopointer(object): def RemoveDuplicates(self, nums, N): if N == 0 or N == 1: return N nums.sort(); i = 1 for j in range(1, N): if nums[j] != nums[j-1]: nums[i] = nums[j] i += 1 lst=[] lst =[0 for f in range(i)] for a in range(i): lst[a] = nums[a] return lstdef test(): ob1 = Twopointer() nums1 = [2,3,4,4,5,6,6,6,7,8,8] nums2 = [1,1,2,3,4,4,5,6,6,7,8,9,9] nums3 = [2,4,4,6,8,10,10] assert ob1.RemoveDuplicates(nums1,len(nums1)) == [2, 3, 4, 5, 6, 7, 8],"Testcase passed" assert ob1.RemoveDuplicates(nums2,len(nums2)) == [1, 2, 3, 4, 5, 6, 7, 8, 9],"Testcase passed" assert ob1.RemoveDuplicates(nums3,len(nums3)) == [2,4,6,8,10],"Testcase passed"if __name__ == "__main__": test() print("Everything passed")Great job getting through this. Let's move on.
If you had any problems with this tutorial, check out the main forum thread here.


