In this tutorial, we are going to discuss three O (n log n) sorting techniques, their implementations, and how we derive their runtimes. The learning objectives of this tutorial are as follows:
- You will be able to apply the
Divide-and-Conquerapproach to different sorting methods. - You will be able to sort an array in
O(N log N)complexity. - We'll learn how to build Max & Min Heaps and apply them to sort an array.
Merge Sort is a divide and conquer algorithm based on the idea of breaking a list down into several sublists until each sublist contains only a single item. Afterwards, we will merge these sublists in such a manner that the resulting list will be sorted.
Essential Idea
- Divide the list into sub-lists, each containing a single element.
- Merge adjacent pairs of two "singleton" (containing only one element) lists to form a
listof 2 elements.- Repeat the above steps, until we get a fully sorted list.
Let's consider an example to understand this approach better.
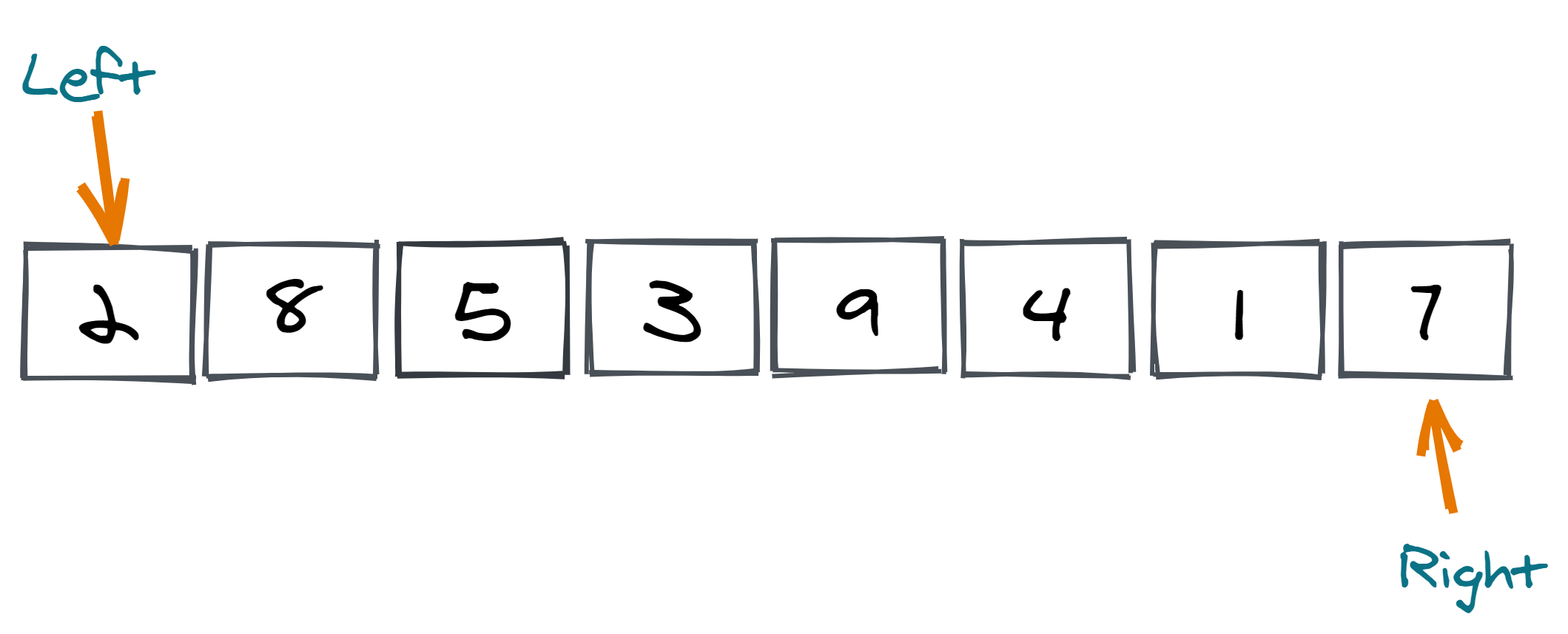
We have an array containing eight elements and two pointers directed at the first and last element.
Dividing the array
One can understand from the images below that at each step, the array of size M is divided into two sublists, of size M/2, until no further division is possible.
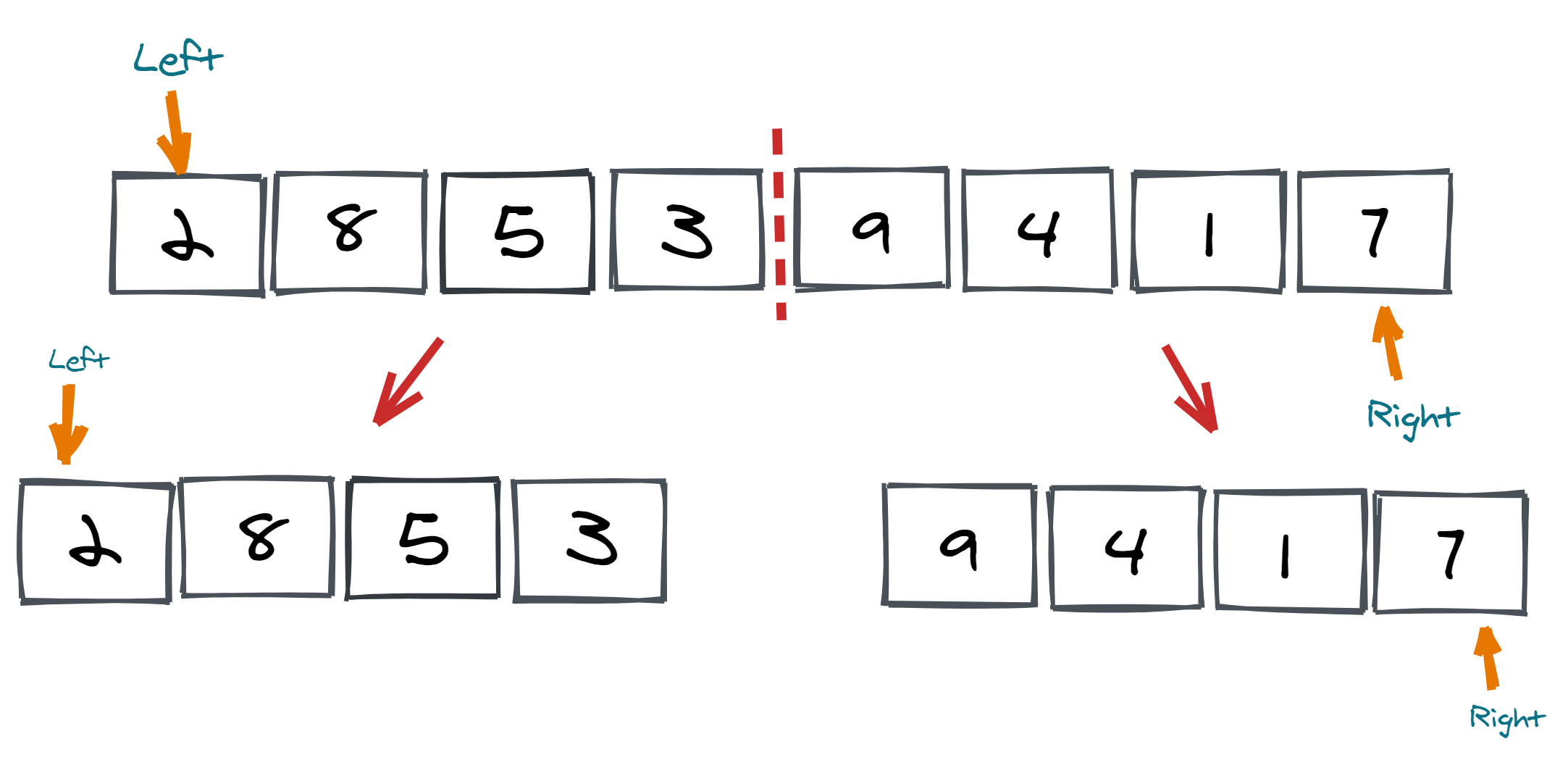
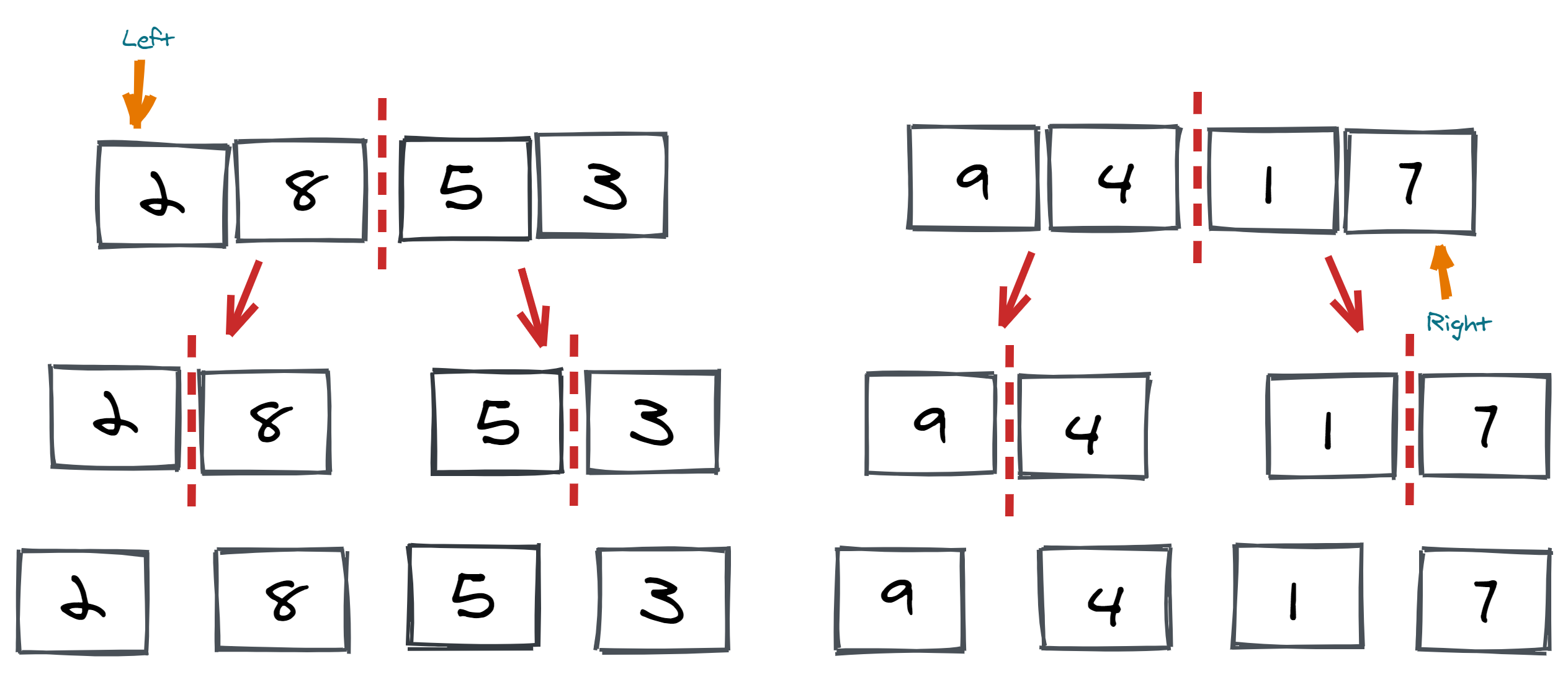
We divide the array using the function merge_sort(array, startIndex, lastIndex). As shown in the images above, merge_sort recursively divided the array into halves until we reach the base case where each subarray contains only single element.
Merging the sub-arrays
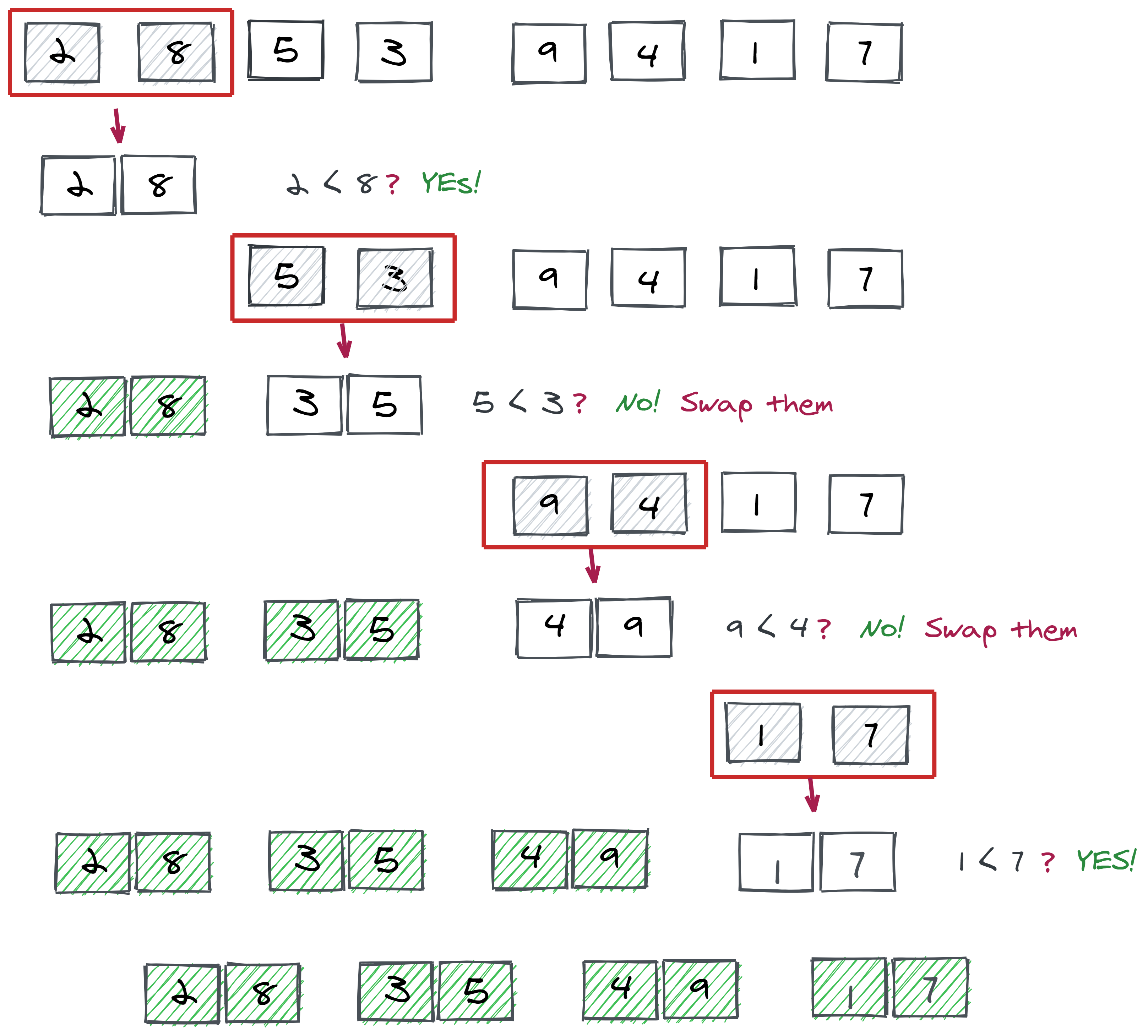
After dividing the array, we will call the merge function that picks up the sorted sub-arrays and combines them to gradually sort the array. This function will also merge the sub-arrays recursively in such a way that a fully sorted array can be obtained.
The below images demonstrates the merging of an array in action.
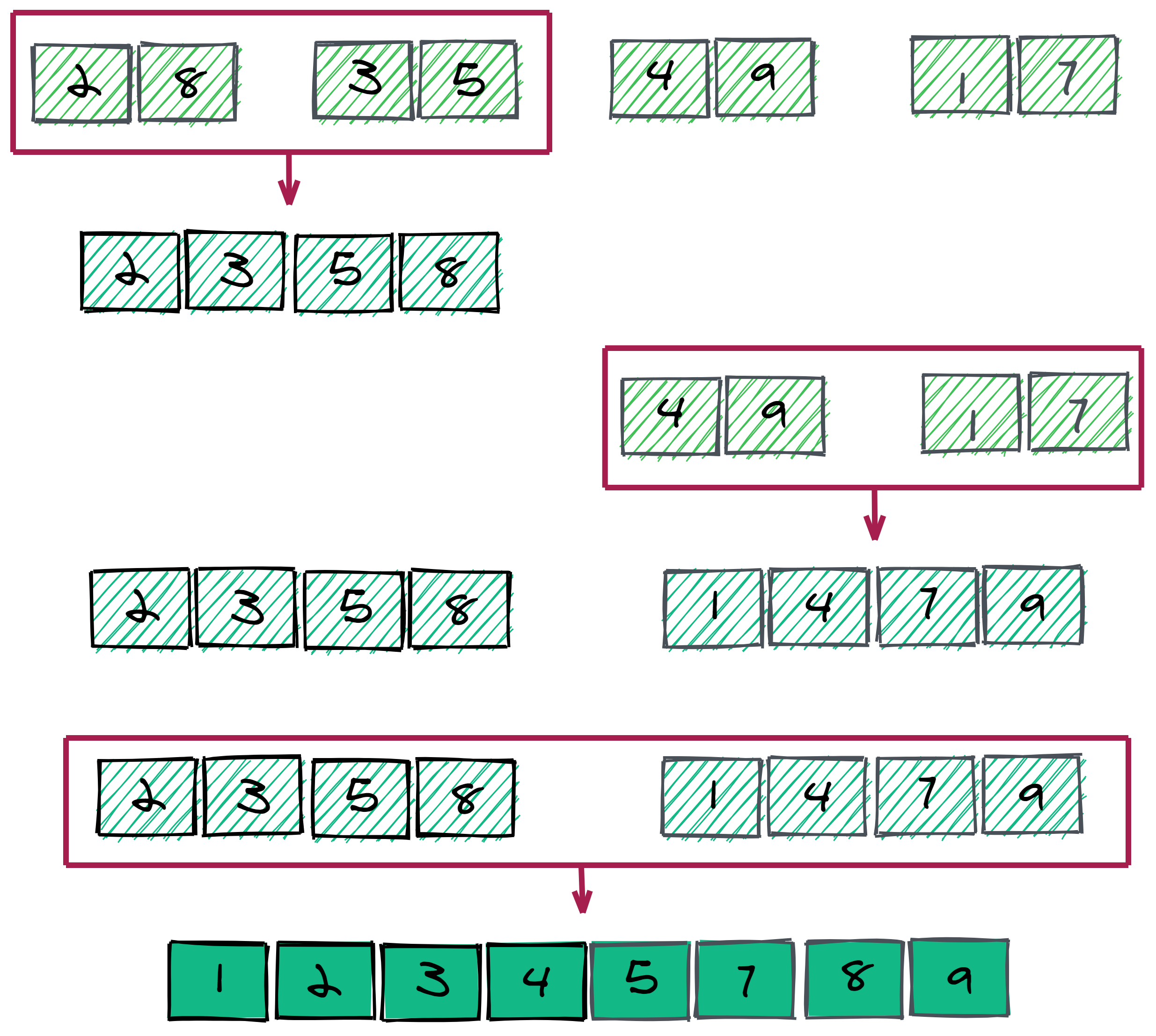
The merge sort can be implemented using the two functions described below.
merge_sort(array, startIndex, lastIndex)merge(array, startIndex, middle, lastIndex)
Here, in the merge function, we will merge two sub-arrays. One sub-array has a range from start to middlewhile the other will go from middle+1 to the last index. We will divide the array into sub-arrays on the merge_sort function.
An implementation of the MergeSort algorithm has been provided below:
xxxxxxxxxxconsole.log(mergeSort([5, 4, 3, 2, 1]));function merge(leftArr, rightArr) { let resultArray = [], leftIndex = 0, rightIndex = 0; // Sort parts while (leftIndex < leftArr.length && rightIndex < rightArr.length) { if (leftArr[leftIndex] < rightArr[rightIndex]) { resultArray.push(leftArr[leftIndex]); leftIndex++; // move left array cursor } else { resultArray.push(rightArr[rightIndex]); rightIndex++; // move right array cursor } } // There will be one element remaining from either left or the right // Concat to account for it return resultArray .concat(leftArr.slice(leftIndex)) .concat(rightArr.slice(rightIndex));}function mergeSort(unsortedArr) { // Only one element base case if (unsortedArr.length <= 1) { return unsortedArr; } // Determine midpoint const midIdx = Math.floor(unsortedArr.length / 2);Time Complexity
The merging of all the sub-arrays into a single array will take O(N) time, while the array of size N can be divided into logN parts, hence the worst case of merge sort is O(N log N).
Build your intuition. Click the correct answer from the options.
The worst-case scenario time complexity of the MergeSort algorithm is:
Click the option that best answers the question.
- O(n)
- O(1)
- O(N logN)
Quick Sort
The quicksort algorithm is based on the divide and conquer technique. We start by:
- Choosing one element as a pivot, and
- Divide the array around it, such that all the elements on the left of the pivot are smaller than the it, and all the elements on the right are greater than the pivot.
How does Quick Sort work?
We will choose a random element from the array as a pivot and swap it with the last element of the array. We will also initialize two pointers left and right pointing to the start and end of the array.
Following this setup, we will rearrange the elements in such a way that the left side of the pivot contains elements that are the smaller and right side of the pivot contains elements that are greater than the pivot. We can accomplish this by following the steps below.
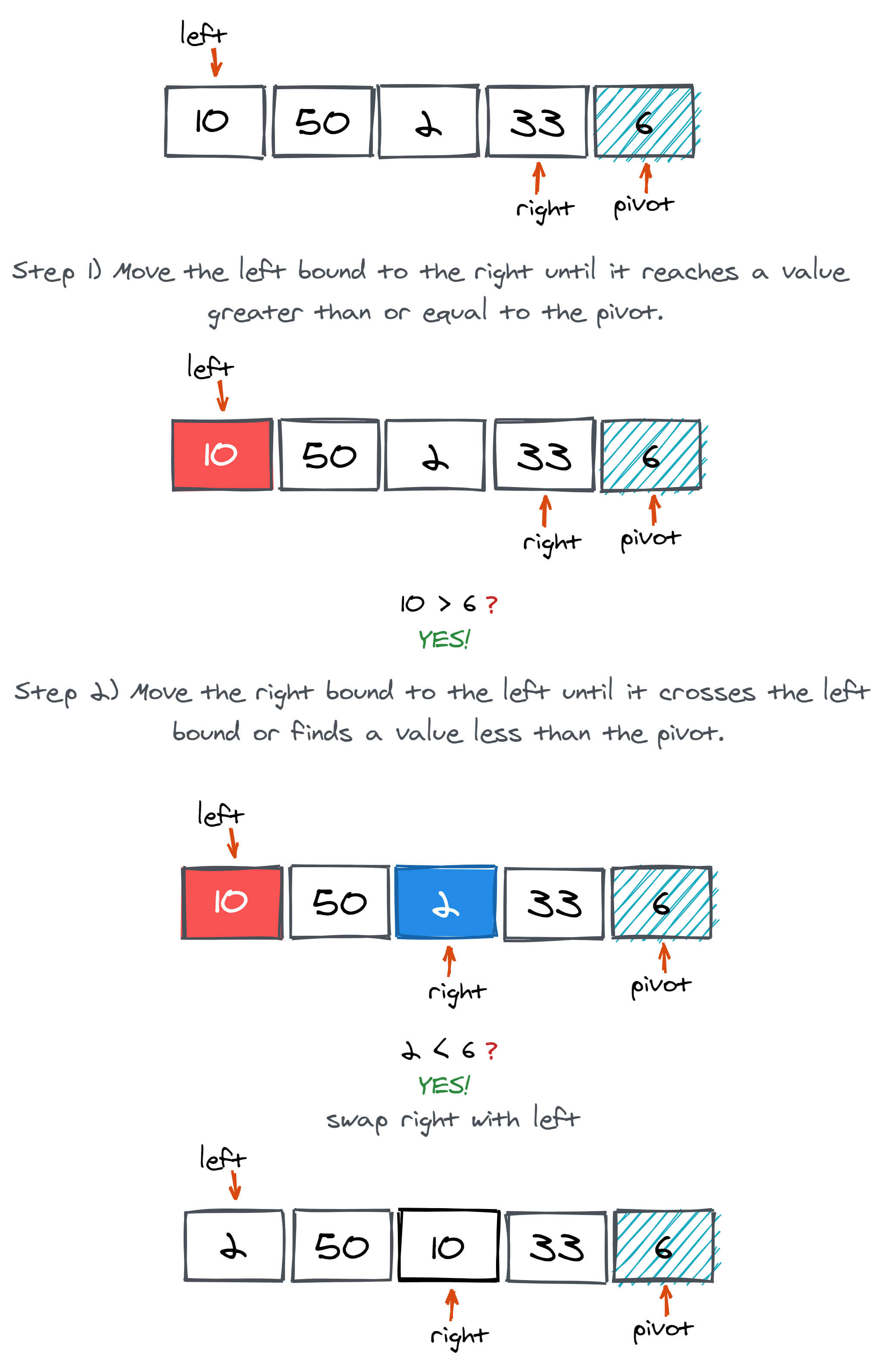
- Move the left pointer to the right until it reaches a value greater or equal to the pivot. Afterward, stop the left pointer and move to step 2.
- Move the right pointer to the left until it crosses the left pointer or finds a value less than the pivot.
- Repeat the above steps until unless both pointers cross each other.
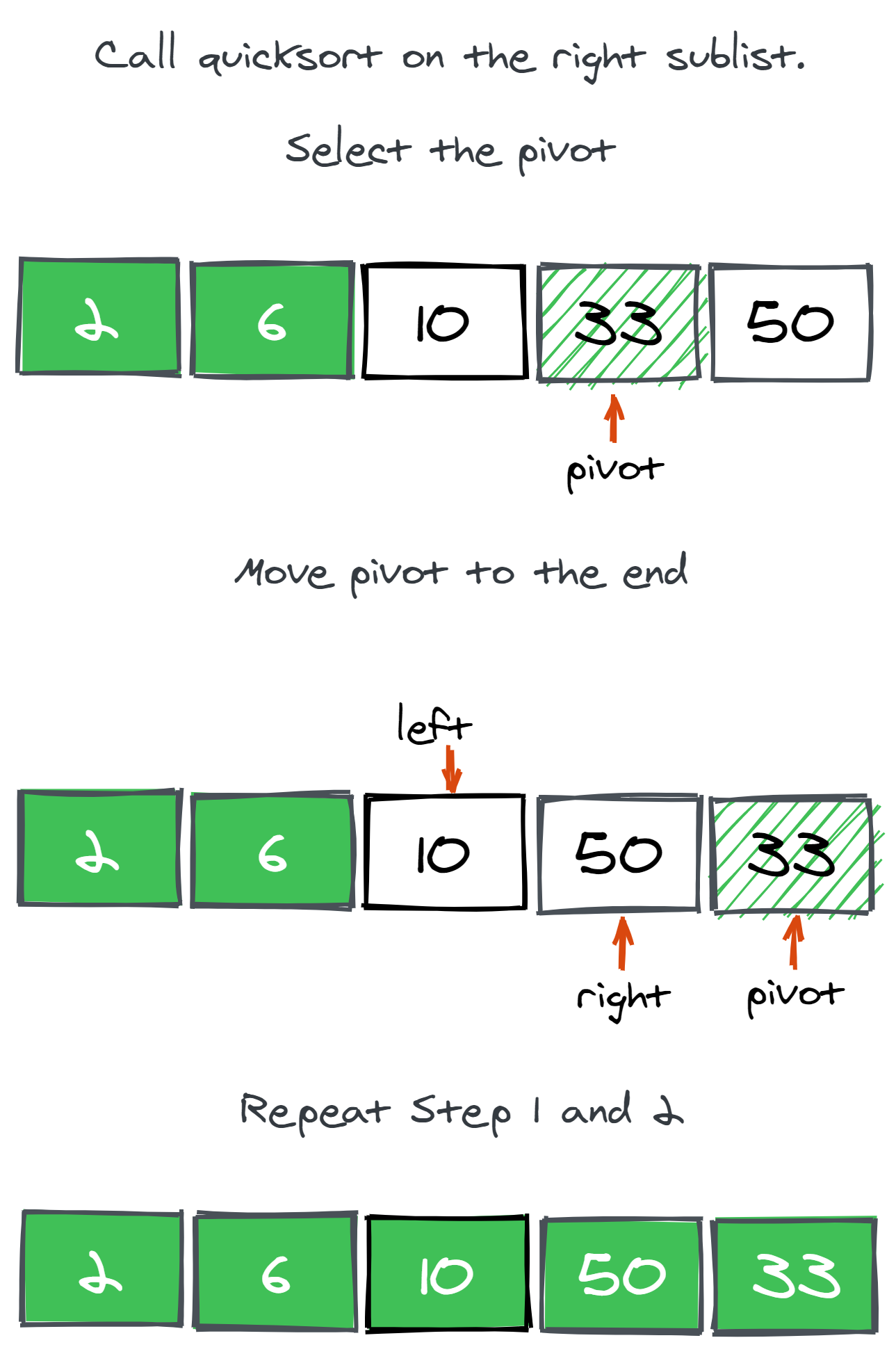
Let's take a look at the following illustrations to understand the approach better. In the figure below, we have chosen the pivot and swapped it with the last element of the array.
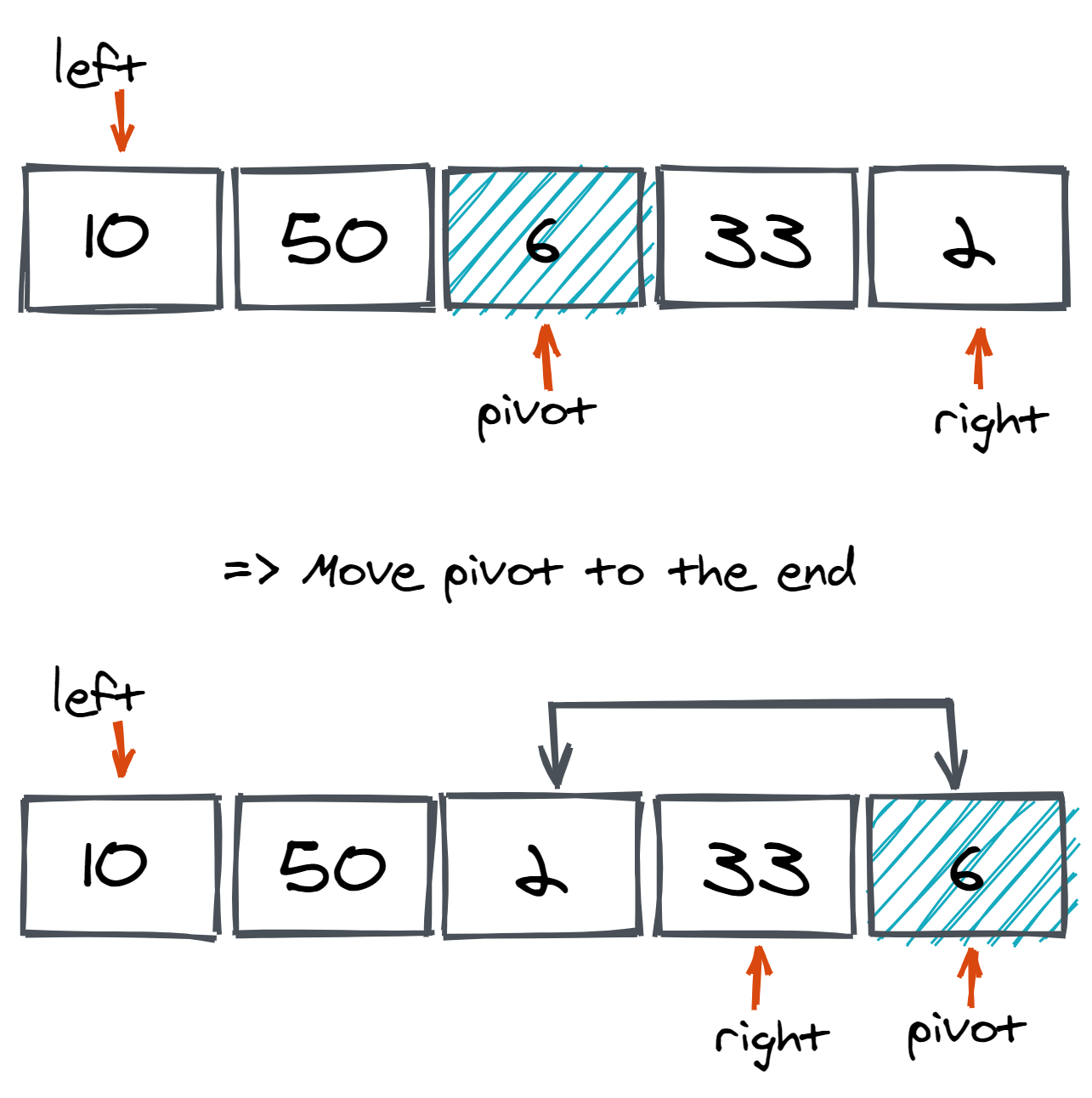
Now, we move the left and right pointer depending on the steps described above. If right < left, then we will swap them.
Now, we can see in the figure below that both pointers crossed each other. Given this, we will mark the element pointed by the left pointer as sorted.
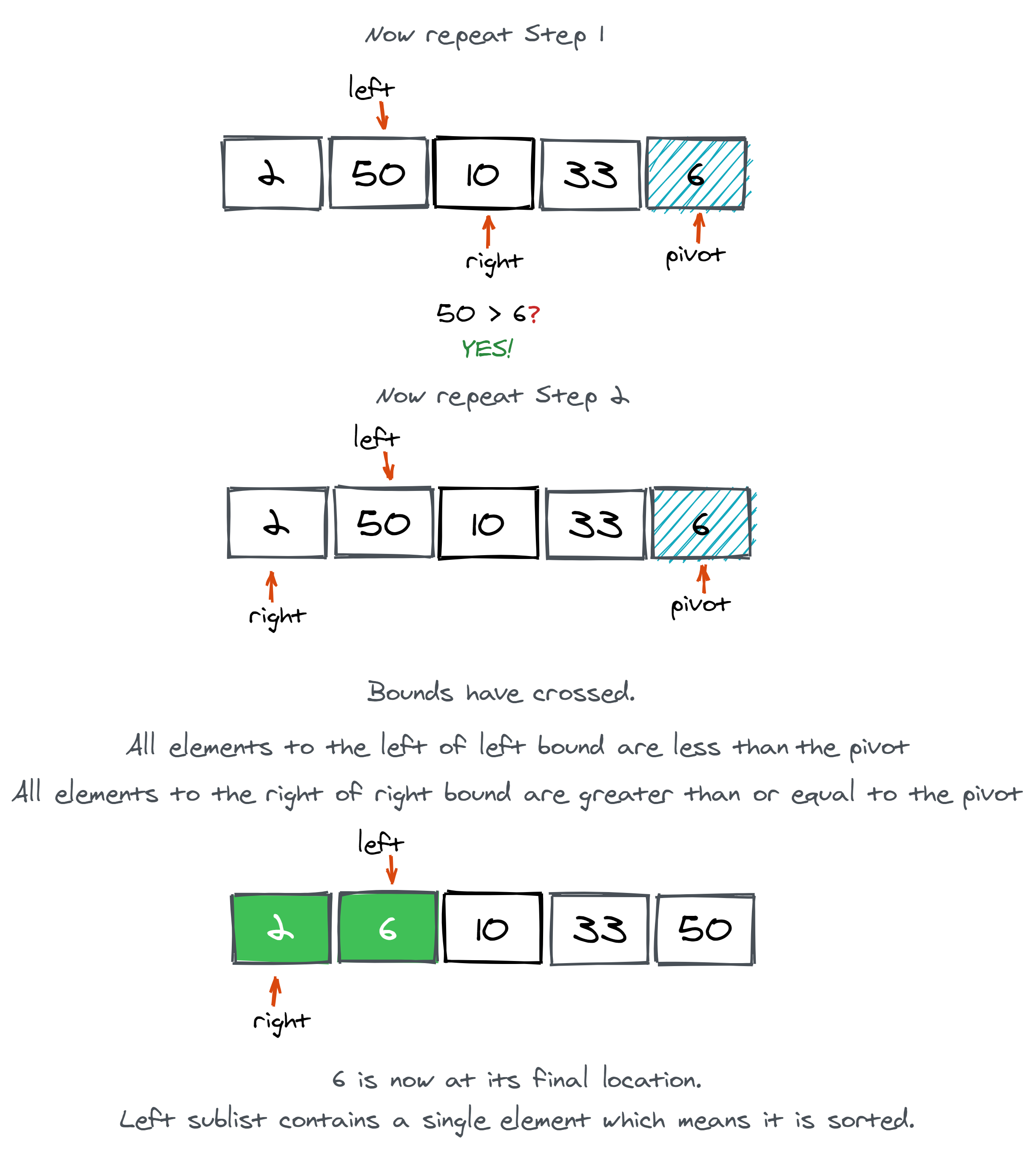
We will then repeat the above steps by first choosing the pivot and swapping it with the last index and so on. At last, we will have all elements sorted.
Implementation of Quick Sort
Quick Sort can be implemented using two functions described below:
- partition(Array, startIndex, lastIndex)
- quick_sort(Array, startIndex, lastIndex)
Here, in the partition function, we are dividing the array based upon the selected pivot. In the quick_sort function, we are re-arranging the elements.
xxxxxxxxxxconsole.log(quickSort(nums, 0, nums.length - 1))function partition(arr, low, high) { let lowIdx = low - 1; let pivot = arr[high]; // pivot for (let j = low; j < high; j++) { // If current element is smaller than or // equal to pivot if (arr[j] <= pivot) { // Increment index of left/smaller element lowIdx = lowIdx + 1; // Swap const temp = arr[lowIdx]; arr[lowIdx] = arr[j]; arr[j] = temp; } } const temp = arr[lowIdx + 1]; arr[lowIdx + 1] = arr[high]; arr[high] = temp; return lowIdx + 1}function quickSort(arr, low, high) { if (arr.length === 1) { // Base case return arr; }Comparison with Merge Sort
With quick sort, there is no need to use the auxiliary array that we used in the merge sort approach. This reduces the space complexity and choosing a random pivot from array improves the time complexity as well.
Let's test your knowledge. Fill in the missing part by typing it in.
Choose a random element from the array as a pivot and swap pivot with the last element of the array. Initialize two pointers left and right pointing to the start and end of the array.
This principle is implemented in which type of sorting algorithm?
Write the missing line below.
Heap Sort
Finally, heap sort is based on comparisons. We can say that it is an improved version of selection sort. It actually visualizes the array elements as heap.
Heap
A heap is a tree-based structure. The definition of one is that it is a complete binary tree and all the nodes are greater than their children. A heap is said to be a Min-Heap if all the nodes are smaller than their children, otherwise it will be considered as a Max-Heap.
How to heapify a tree?
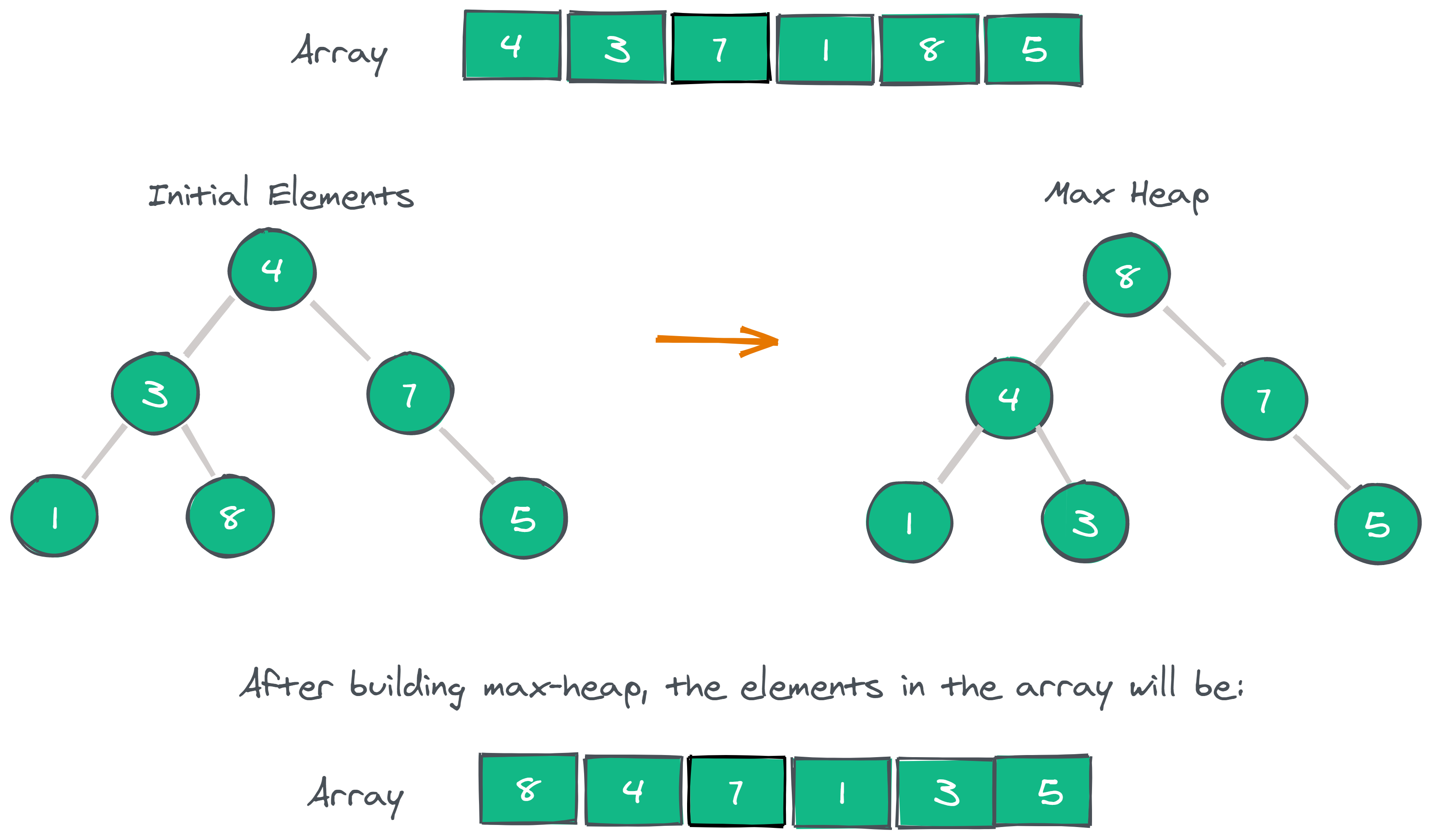
A function called heapify can be used on all non-leaf nodes of the heap in order to make a Max-Heap.
Implementation of HeapSort
Consider an Array which is to be sorted using heap sort. To begin, we will create Max-Heap using the elements of Array.
The first element of the array would be the largest, so we will swap this element with the last one. We will heapify the Max-Heap but exclude the last element as it is already in its correct position. After that, we will decrease the length of the array by one. Then, we will repeat this step until all the elements in the array are in their correct position.
The following steps should be taken in order to sort the above Array.
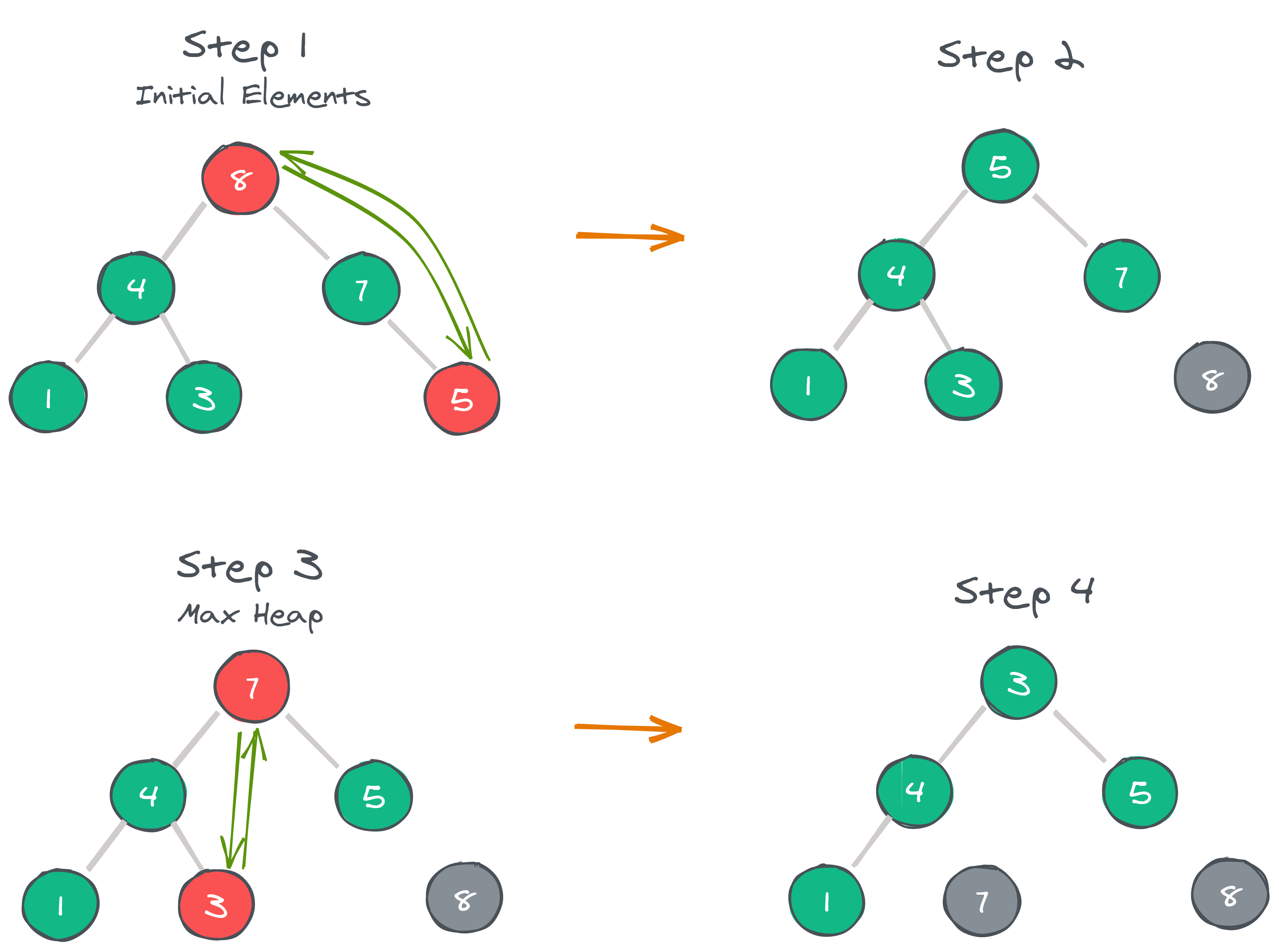
Step 1: 8 is swapped with 5.
Step 2: 8 is disconnected from the heap as 8 is in the correct position now and.
Step 3: Max-heap is created and 7 is swapped with 3.
Step 4: 7 is disconnected from the heap.
Step 5: Max heap is created and 5 is swapped with 1.
Step 6: 5 is disconnected from the heap.
Step 7: Max heap is created and 4 is swapped with 3.
Step 8: 4 is disconnected from the heap.
Step 9: Max heap is created and 3 is swapped with 1.
Step 10: 3 is disconnected
The following illustrations will demonstrate the above steps.
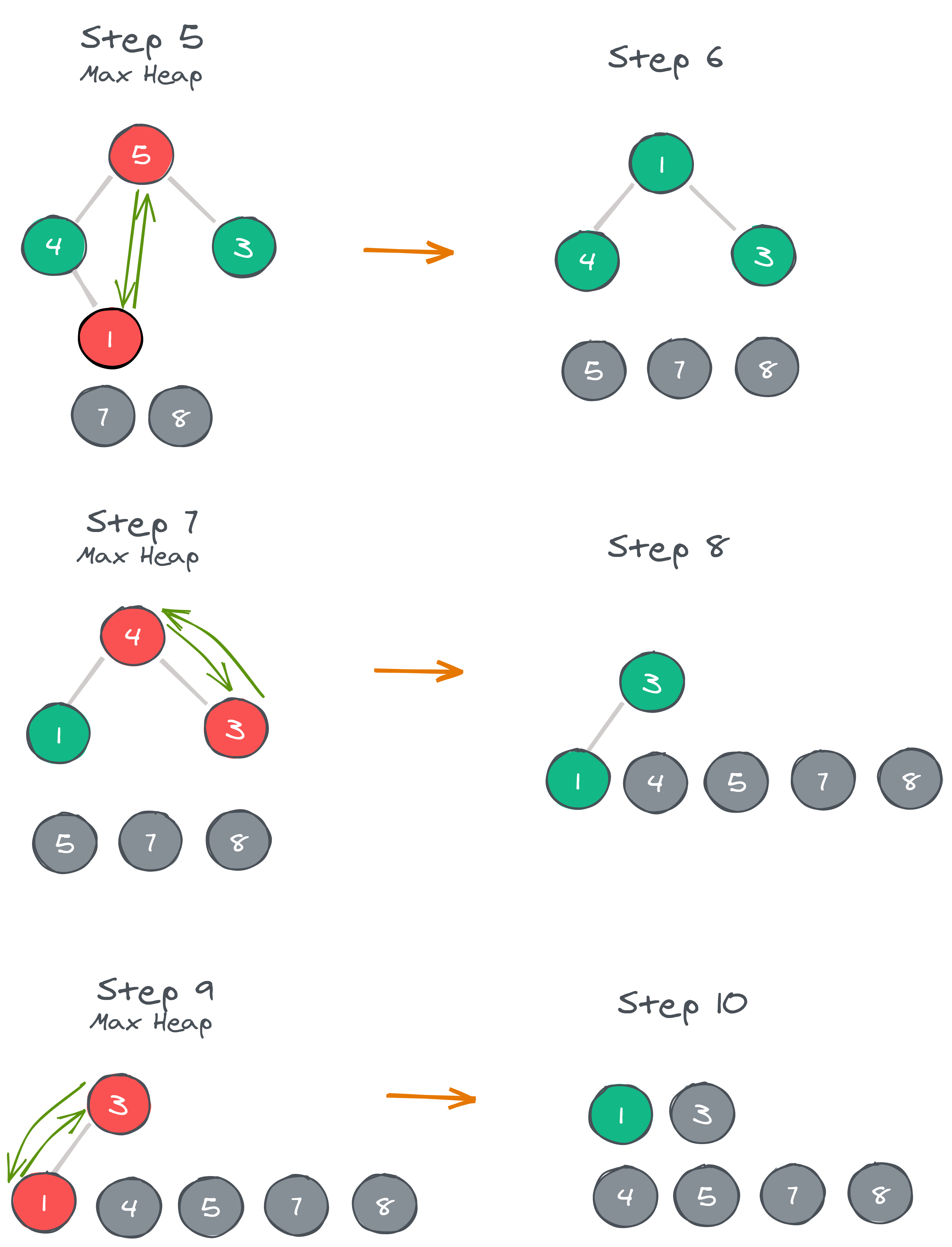
After all the steps, we will get the sorted array.

In C++, the following functions will be used to implement Heap Sort.
- heapify(Array, size, index)
- heapSort(Array, size)
The heapify function will convert all non-leaf nodes of the heap to Max-Heap and heapSort will first create a priority queue, and then repeatedly pop the elements from the heap until it becomes empty.
Implementation of HeapSort has been provided below:
xxxxxxxxxxconsole.log(heapSort([4, 11, 1, 21, 34, 85, 6, 49, 7, 12, 31]));const heapSort = function(arr) { const n = arr.length; for (let i = Math.floor(n/2) - 1; i >= 0; i--) { heapify(arr, n, i); } for (let i = n - 1; i >= 0; i--) { swap(arr, 0, i); heapify(arr, i, 0); } return arr;}const heapify = function(arr, n, i) { // find places in array heap let left = 2 * i + 1; let right = 2 * i + 2; if (left >= n && right >= n) { return; } const leftValue = (left >= n) ? Number.NEGATIVE_INFINITY : arr[left]; const rightValue = (right >= n) ? Number.NEGATIVE_INFINITY : arr[right]; if (arr[i] > leftValue && arr[i] > rightValue) { return; } if (leftValue > rightValue) { swap(arr, i, left); heapify(arr, n, left);Let's test your knowledge. Is this statement true or false?
A function called heapify can be used on all nodes of the heap in order to make a Max-Heap, no matter the node types.
Press true if you believe the statement is correct, or false otherwise.
Complexity of HeapSort
Heap sort has the time complexity of O(N log N) for all cases.
Note that heap sort is not stable. Stable sorting allows us to sort based on more than one key. Operations in the heap can change the relative order of equivalent keys-- picture the event of two identical numbers in the heap, which make their way to different locations.
Are you sure you're getting this? Click the correct answer from the options.
Which of the following sorting algorithms is based on the divide-and-conquer principle?
Click the option that best answers the question.
- MergeSort
- QuickSort
- HeapSort
- All of the above
One Pager Cheat Sheet
- We will learn how to use the
Divide-and-Conquerapproach and apply it to sort an array inO(N log N)complexity using Max & Min Heaps. - Merge Sort is an efficient
divide and conqueralgorithm that breaks down lists into smaller sublists, sorts them, and then merges them in order to create a fully sorted list. - The MergeSort algorithm can be implemented using two functions -
merge_sort(array, startIndex, lastIndex)andmerge(array, startIndex, middle, lastIndex), which divides and merges sub-arrays. - The sorting of an array of size
Nusing Merge Sort has a worst-case time complexity ofO(N log N). - The worst-case time complexity of MergeSort is
O(N logN), resulting from the merging ofNelements and the splitting of each element intologNparts. - The Quick Sort algorithm is based on the
divide and conquertechnique, whereby apivotelement is chosen, and the array is divided into two sides, with elements on the left being smaller than the pivot, and elements on the right being greater. - Quick Sort can
be implementedusing two functions,partitionandquick_sort, to divide and re-arrange elements in the array based on a selected pivot. - Quick sort reduces the
space complexityand improves thetime complexityby using an random pivot selection from the array, compared to merge sort. - Quick Sort uses a
partitioningprocess to split the unsorted array around a randomly chosen pivot element and recursively sort the subarrays. - Heap Sort is an improved version of
selection sortwhich views theArrayas a Max-Heap and utilizes aheapifyfunction to put the elements in their correct positions. - The
heapifyandheapSortfunctions are used to implement Heap Sort in C++. - The
heapifyfunction can only be used on non-leaf nodes to convert them to aMax-Heap, as leaf nodes have no children to be converted. - Heap sort has a time complexity of
O(N log N), but is not stable. - Both Merge Sort and Quick Sort are popular sorting algorithms based on the
divide-and-conquerprinciple, where a problem is broken down into smaller sub-problems and then combined to get the desired result.

