In this tutorial, we'll look at yet another technique for finding an optimal solution to a problem. Dynamic programming considers all the solutions of a problem and selects the best or optimal one. But despite finding the most efficient solution, the problem is still speed and memory. For a large problem, it could take a long time to solve, and in some cases, may consume too much memory.
Greedy algorithms are designed for speed. When given a sub-problem, a greedy algorithm chooses the local best solution and moves towards the final goal, hoping this strategy would closely approximate the "global" optimal solution.
This sounds great, but one thing to keep in mind is that greedy algorithms do not always get us the most optimal solution for some problems. They may give a sub-optimal solution in such cases. However, there are problems for which it is proven that greedy algorithms do provide the best solution, which makes them awesome fits of strategy in certain situations.
In this tutorial, I will give examples of problems, where the greedy algorithm gives a sub-optimal solution, along with problems for which it gives an optimal answer.
Finding the Path With Maximum Reward
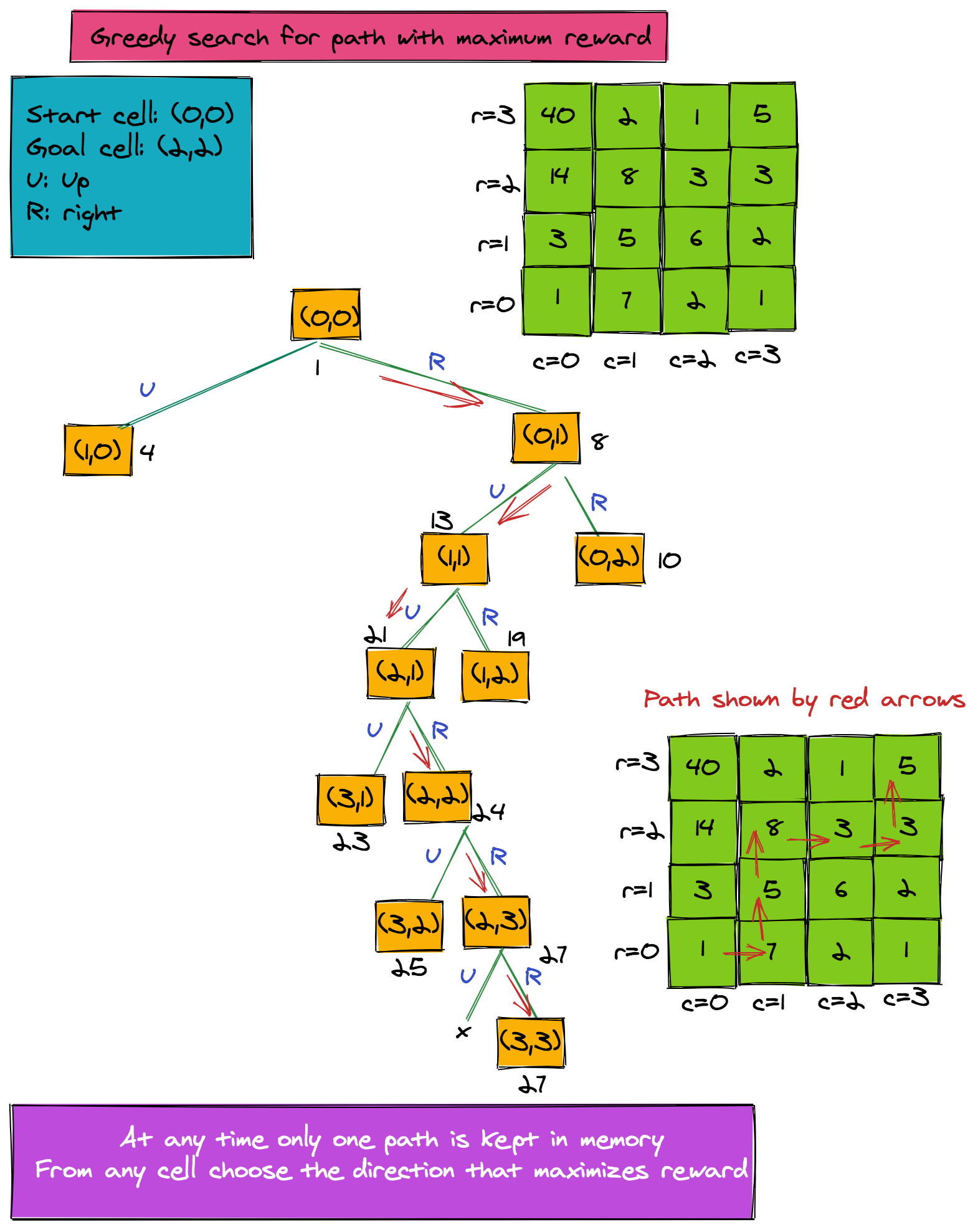
Suppose we have a robot that is placed at cell (0, 0) of an m * n grid. The robot has to navigate the grid and reach its goal position, while collecting a reward from each cell it passes through. The aim of navigation is to follow a path that maximizes the reward through the grid. The only legal moves allowed are an "up" move and a "right" move.
This tutorial on dynamic programming has an informative illustration on how to find a path through a grid to maximize reward. Both time complexity and space complexity of the dynamic programming solution are O(m * n).
Greedy Algorithm for Maximizing Reward
The greedy algorithm for maximizing reward in a path starts simply-- with us taking a step in a direction which maximizes reward. It doesn't keep track of any other path. The algorithm only follows a specific direction, which is the local best direction. The pseudo-code for the algorithm is provided here.
The figure below illustrates how a greedy algorithm solves the problem. The hope is that by taking the locally best solutions, we ultimately approximate the global best solution.
Note that for this problem, a greedy search through the grid does not give us the optimal solution. We can see that the cell (3, 0) has a reward of 40, and our algorithm never passes through this cell.
Complexity of Greedy Navigation Through the Grid
For any path, there are (m-1) up moves and (n-1) right moves, hence the total path can be found in (m+n-2) moves. Therefore the complexity of the greedy algorithm is O(m+n), with a space complexity of O(1). It is very tempting to use this algorithm because of its space and time complexity-- however, there are no guarantees that it would give the most optimal accumulated reward.
1routine greedyNavigate
2Input: Matrix w of dimensions m * n containing reward for each cell,
3Start cell coordinates: (0, 0)
4Goal cell coordinates: (m-1, n-1)
5Output: Path found and the accumulated reward on that path
6
7// (r, c) denotes (row, column) coordinates
81. total = 0
92. (r, c) = (0,0)
103. while (r, c) != goal
11 a. total = total + w[r, c]
12 b. print (r, c) // print coordinates of the cell
13 // check if we are in top row
14 c. if (r == m-1)
15 c = c+1 // go right. no other choice
16 // check if we are in rightmost col
17 d. if (c == n-1 )
18 r = r+1 // go up, no other choice
19 // greedily select either up or right move
20 e. if w[r+1, c] > w[r, c+1]
21 r = r+1 // move up
22 else
23 c = c+1 // move right
244. Print goal
255. return total // return accumulated rewardxxxxxxxxxxlet total = 0;let r = 0, c = 0;while (r !== m-1 || c !== n-1){ total += w[r][c]; console.log(r + ", " + c); if (r === m-1) c++; else if (c === n-1 ) r++; else if (w[r+1][c] > w[r][c+1]) r++; else c++;}console.log(m-1 + ", " + (n-1));return total;Activity Selection Problem
A problem for which a greedy algorithm does work and gives the optimal solution is the activity selection problem. There is a weighted version of the same problem, discussed here, which cannot be solved using a greedy algorithm. However, its unweighted version that we discuss here can be solved optimally using a greedy strategy.
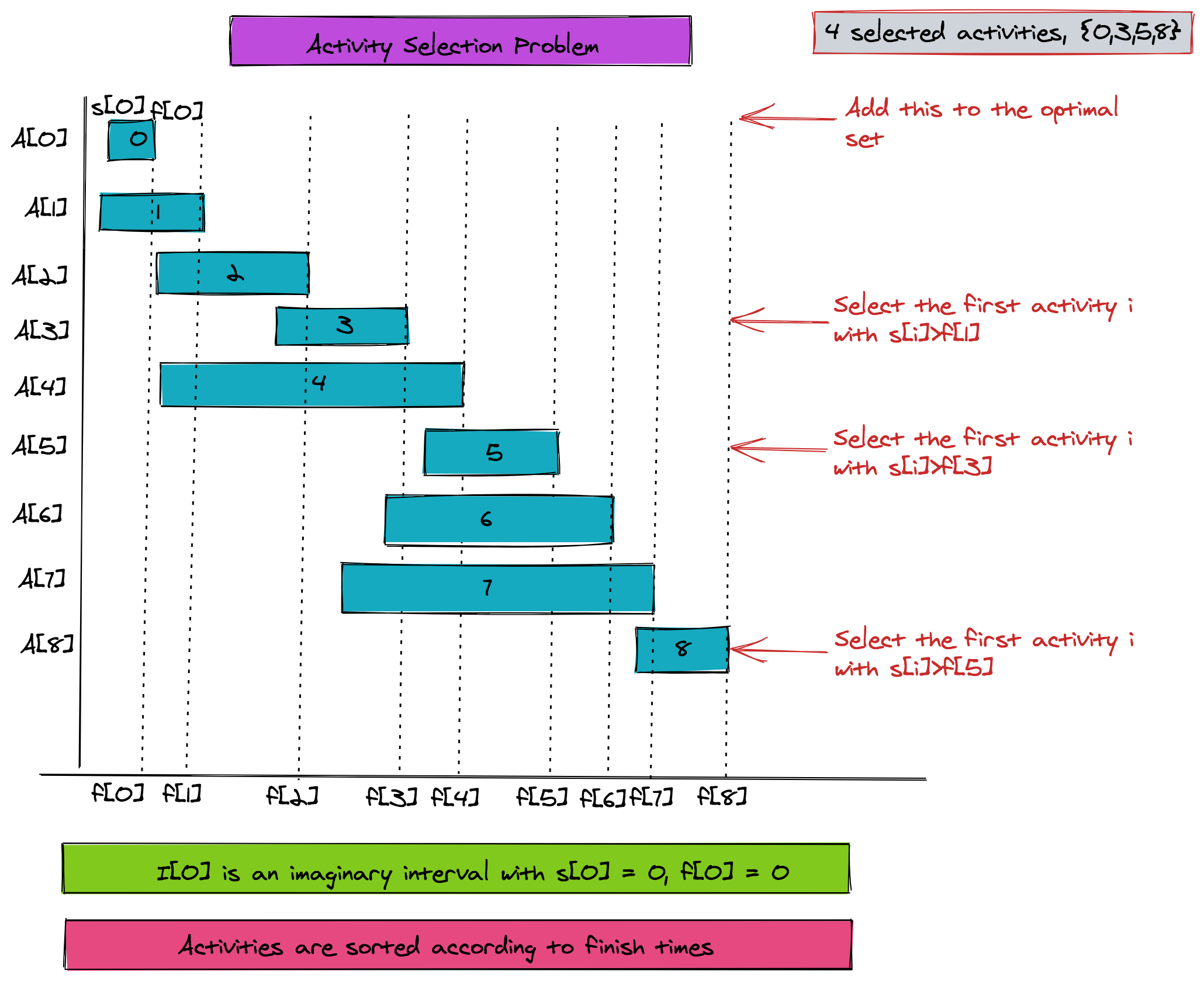
The activity selection problem involves a set of n activities, each having a start and finish time. Some of these activities are overlapping. The objective is to select a maximum sized set of non-overlapping activities.
The following are the parameters of this problem:
nis the total number of intervals- Array
sandfof sizento store the start and finish time of each activity s[j] < f[j]forj = 0..(n-1)- The arrays are sorted according to finish time values (in
farray) in ascending order
Greedy Algorithm for Activity Selection
Here is the pseudo-code that solves the activity selection problem using a greedy strategy. We may assume that the intervals are sorted according to their finish times.
The problem parameters along with the solution are both shown in the figure below. The algorithm first adds activity 0 to the selected pool. Next, it iteratively finds the first activity whose start time is greater than the finish time of the last added activity. It then adds it to the pool.
Time Complexity of Activity Selection
If we analyze the pseudo-code, we can see that only one pass is made through all the activities and hence the time complexity is O(n). There is no additional intermediate space involved for storing an array or matrix, making it O(1) space complexity.
However, we made an initial assumption that the activities are sorted according to finish times. If the activities are not sorted, then we can add O(n log n) overhead for sorting, making the time complexity O(n log n) and space complexity O(1).
1Routine selectActivity
2Input: Finish time array f
3Output: Selected activity array S and total activities in S
4
51. count = 0
62. S[count] = 0
73. lastInd = 0 // index of last activity added to S
84. for i = 1..(n-1)
9 a. if s[i] >= f[lastInd] // add i to selected activity set S
10 then
11 {
12 i. count = count + 1
13 ii. S[count] = i
14 iii. lastInd = i
15 }
165. return (count + 1) and Sxxxxxxxxxxfunction selectActivity(f) { let count = 0; let S = []; S[count] = 0; let lastInd = 0; // index of last activity added to S for (let i = 1; i < f.length; i++) { if (f[i] >= f[lastInd]) { count = count + 1; S[count] = i; lastInd = i; } } return [S, count + 1];}Fractional Knapsack Problem
Our last example is that of the fractional knapsack problem. There are many versions of this problem. You can look at one variant of the same problem called the coin change problem, which can be solved via dynamic programming.
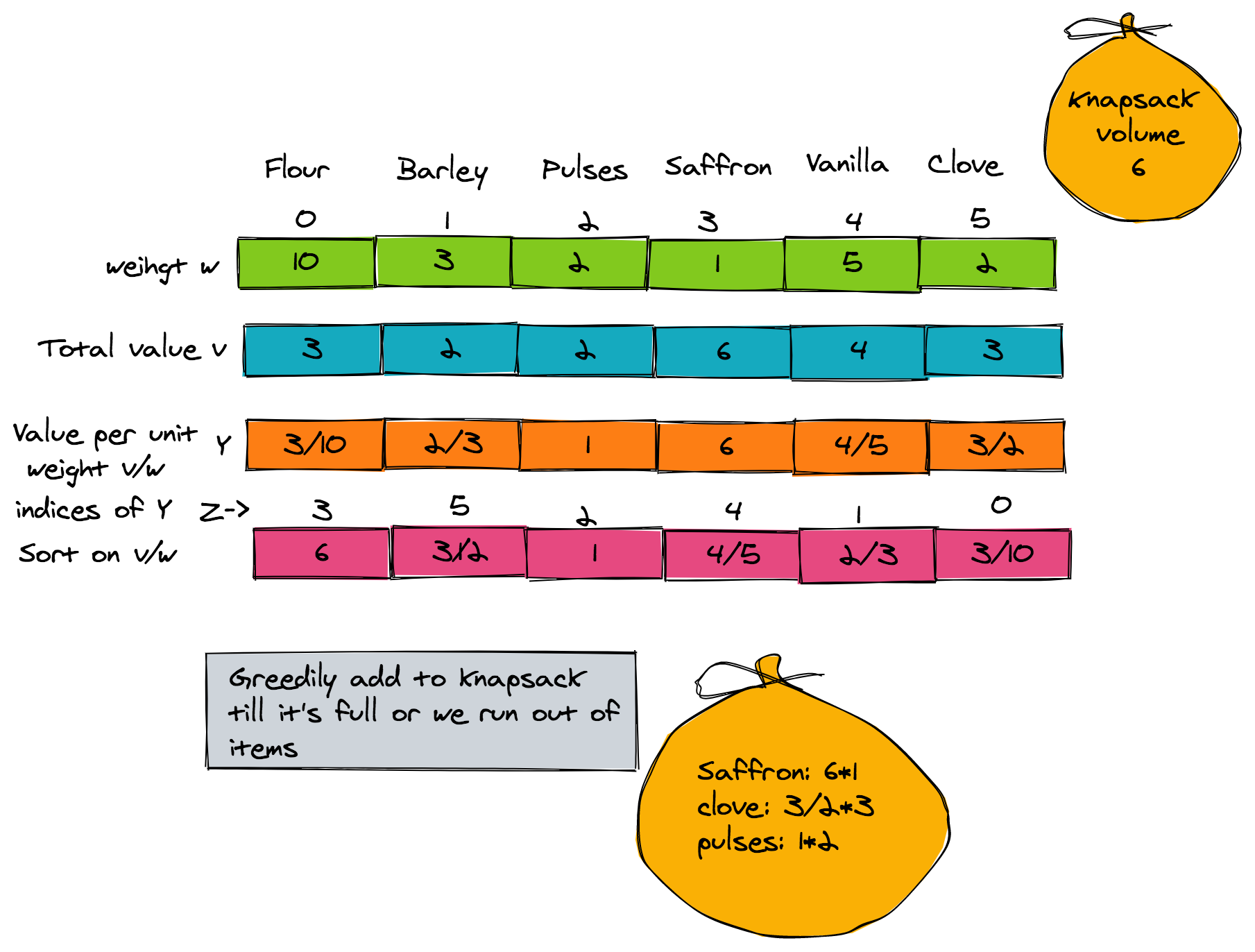
For the fractional knapsack problem, we can assume that there is a warehouse with n items, and we maintain two arrays:
vas the values of the itemswas the weights of the items
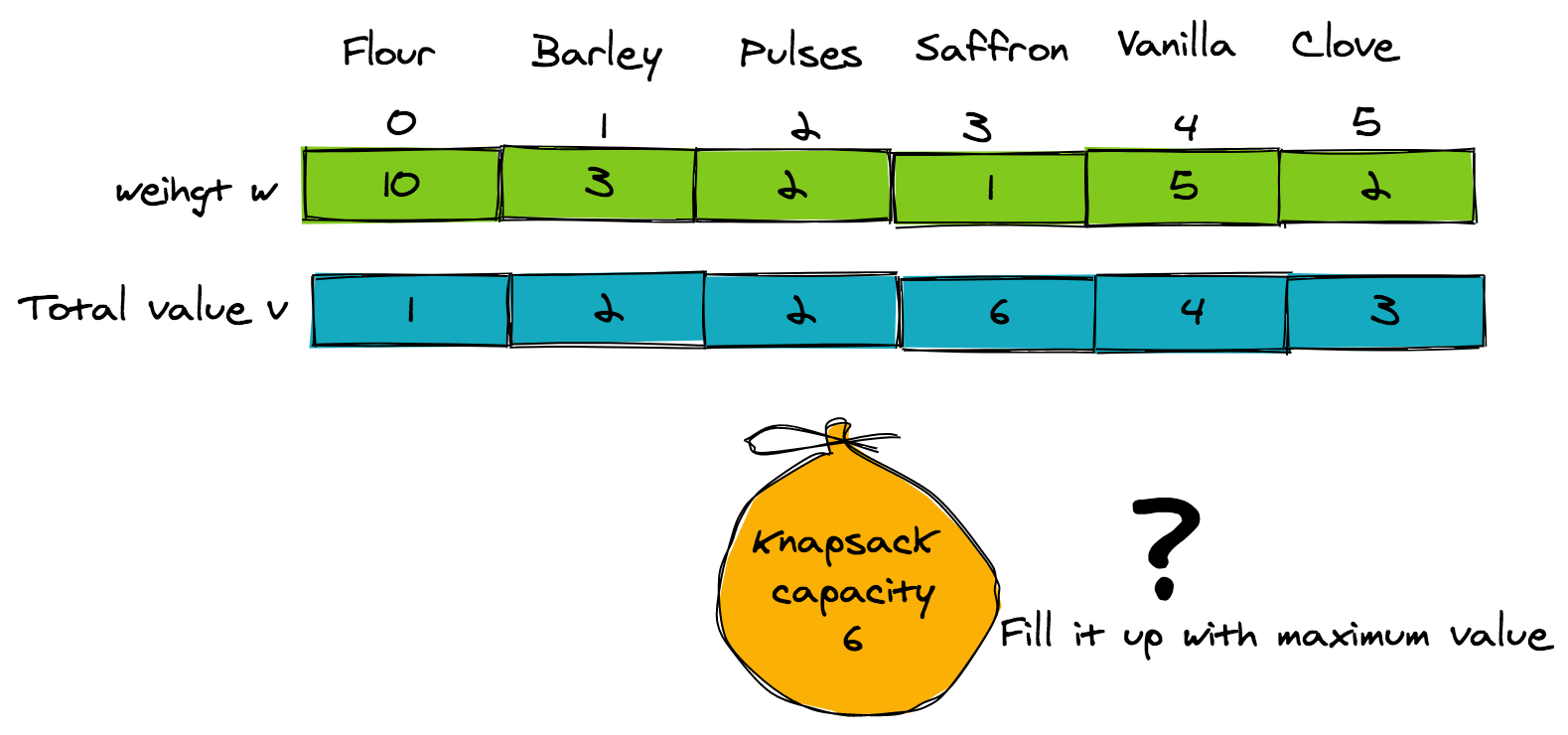
So here the ith item has a value of v[i] and a total weight of w[i]. Suppose a thief enters the store with a knapsack, which has a weight capacity X. The goal is to find out how to fill the knapsack so that the total items in the sack have a maximal value. This example problem is shown in the figure below:

Greedy Solution of Fractional Knapsack Problem
There is an amazing method of solving the fractional knapsack problem which uses a greedy strategy. This greedy algorithm first computes the value per unit weight of every item (i.e. v/w). It then sorts v/w in descending order. After that comes the stage for filling the sack greedily-- by adding items in order of decreasing v/w values.
The pseudo-code of the solution is attached here.
Complexity of Fractional Knapsack Problem
In the pseudo-code we can see that step 8 scans each item only once, with O(n) running time. However, step 3 involves sorting, which has a running time complexity of O(n log n). Thus, the overall time complexity is O(n log n) and space complexity is also O(n). This is because we are using one additional array for storing v/w and another one for keeping the sorted indices.
1Routine: solveKnapsack
2Input: Weight array w, value array v of size n,
3 X = capacity of knapsack
4Output: Array R containing indices of items in the sack and
5 array Rwt that has the corresponding weight of
6 each item in the sack,
7 val: total value of items in sack,
8 RInd: total items added in sack
9
101. Initialize array R to -1 and array Rval to zero
112. Create an array Y containing value of each item per unit of weight
12 Y[i] = v[i]/w[i] for i = 0..(n-1)
133. Create an array Z, which has indices of the sorted values of Y in descending order.
144. remaining = X
155. i = 0
166. val = 0
177. RInd = 0
188. while (i < n and remaining < X)
19 a. toadd = min(remaining, w[Z[i]])
20 b. R[RInd] = Z[i]
21 c. Rwt[RInd] = toadd
22 d. val = val + val[Z[i]] * toadd
23 e. remaining = remaining - toadd
24 f. i = i+1
25 g. RInd = RInd + 1
269. return R, Rwt, val, RIndxxxxxxxxxxpublic class Knapsack{ public (List<int> R, List<int> Rwt, float val, int RInd) SolveKnapsack(List<int> w, List<float> v, int X) { int n = w.Count; List<int> R = new List<int>(new int[n]); List<float> vPerW = new List<float>(new float[n]); for (int i = 0; i < n; i++) vPerW[i] = v[i] / w[i]; List<int> idx = Enumerable.Range(0, vPerW.Count()).ToList(); idx.Sort((i, j) => vPerW[i].CompareTo(vPerW[j])); idx.Reverse(); int remaining = X, i = 0, RInd = 0; float val = 0; while (i < n && remaining < X) { int toAdd = Math.Min(remaining, w[idx[i]]); R[RInd] = idx[i]; val += v[idx[i]] * toAdd; remaining -= toAdd; i++; RInd++; } return (R, w, val, RInd); }}Try this exercise. Click the correct answer from the options.
Which of the following statements are true?
Click the option that best answers the question.
- Greedy algorithms always return optimal result
- Greedy algorithms are efficient in terms of time and space
- Greedy algorithms can search for the shortest path in a graph, but there are no guarantees of finding it
- Both options 2 and 3
Are you sure you're getting this? Click the correct answer from the options.
For the problem of path finding through the grid, if we change the goal cell to (m-1, 0)-- which of the following holds true?
Click the option that best answers the question.
- There is a possibility that the greedy algorithm will not find the goal
- Greedy algorithm will always find the goal
- Greedy algorithm will always find the goal with maximum reward
Let's test your knowledge. Click the correct answer from the options.
For the interval scheduling problem. If all intervals overlap, then how many intervals will be in the selected set when using greedy algorithm?
Click the option that best answers the question.
- Only one interval
- All intervals
- Only the first and last interval
One Pager Cheat Sheet
- In this tutorial, we'll explore the differences between using
Dynamic programmingand Greedy algorithms to find optimal solutions to problems, noting that the latter can sometimes lead to suboptimal solutions. - The tutorial on dynamic programming provides an example of finding a path through a grid to maximize reward with
O(m * n)time complexity and space complexity. - The greedy algorithm takes the
local bestsolutions with the hope of approximating the global best solution in a path, but withO(m+n)time complexity andO(1)space complexity, there are no guarantees that it will result in the most optimal accumulated reward. - A greedy algorithm can provide the optimal solution for the
activity selection problem, which involves selecting a maximum sized set of non-overlapping activities from a set ofnactivities with given start and finish times. - The greedy algorithm for activity selection has
O(n)time complexity withO(1)space complexity, assuming the intervals are already sorted by finish times; otherwise, this hasO(n log n)time complexity withO(1)space complexity. - The goal of the fractional knapsack problem is to find out how to fill a knapsack with a weight capacity
Xso that the total items in the sack have a maximal value. - The Fractional Knapsack Problem has an efficient
greedystrategy-based solution withO(n log n)time complexity andO(n)space complexity. - The running time complexity of the fractional knapsack problem is
O(n log n)and the space complexity isO(n). - The greedy algorithm may not find the
optimal pathto the goal if the goal is changed to(m-1, 0)due to its reliance on an evaluation function to choose theshortest path to the goal. - The greedy algorithm for interval scheduling only selects
one intervalwith the earliest finish time in each iteration.

