The Marvel of Binary Trees: Understanding the Basics

What is a Binary Tree?

A Binary Tree is a specialized tree structure where each node has, at most, two child nodes. Interestingly, a binary tree can also be empty, meaning it has zero nodes.

The Recursive Nature of Binary Trees

One of the most intriguing aspects of binary trees is their recursive structure. What does this mean? Well, if you have a rule that applies to the tree, you can also apply that rule to each of its subtrees. In essence, each subtree is a smaller binary tree within the larger structure!

The Heart of a Binary Tree: The Node

To represent a binary tree, you really only need one data structure, aptly called a Node. A node will have:

• A Key: The data or value that the node holds.
• Left Child: A pointer or reference to the left child node.
• Right Child: A pointer or reference to the right child node.

Importance of the Root Node

The root node serves as your gateway to the entire tree. You can traverse to any other node starting from the root. A common pitfall for beginners is losing track of the root node, which makes the entire tree inaccessible. So, it's good practice to maintain a pointer to the root node and ensure it's not modified recklessly in the code.

1# Node definition
2class Node:
3    def __init__(self, val):
4        self.val = val
5        self.left = None
6        self.right = None

Here, we are assuming that key data type is an integer, just to keep things simple. But it should be noted that the key type can be any data structure which allows comparison operators, i.e.., <, >, >=, <=, ==.

Binary Search Trees

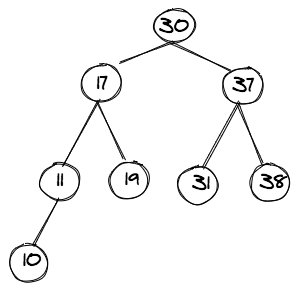
Binary search trees (or BST for short) are a special case of binary trees, which have an added constraint on the placement of key values within the tree. Very simply, a BST is defined by the following rule:

• All nodes in the left subtree have key values less than the key value of the parent
• All nodes in the right subtree have key values greater than the key value of the parent

The figure below shows an example of a binary search tree:

If you want to allow duplicate keys to a binary tree, you can do so as long as you be consistent in your implementation. That means you can either always add duplicate nodes to the left, or to the right. But not both in the same tree.

Balanced BST

A balanced BST is a BST in which the difference in heights of the left and right subtrees is not more than one (1). These example diagrams should make it clear.

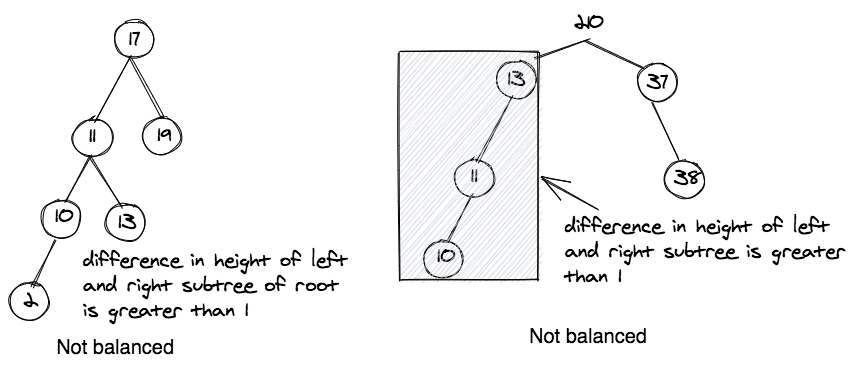
Note: Balanced binary tree does not support duplicate keys by default. But if you still want to add duplicates to a balanced binary tree, you can do so by keeping a count of the number of keys in a Node and incrementing it instead of adding a new Node. This is left as side work for you. Post a comment on the discussion if you implemented this!

The Art of Balancing a Binary Search Tree (BST)

Transforming an unbalanced BST into a balanced one might seem like a daunting task, but it's simpler than you might think. This process gains particular importance when we want to optimize the performance of operations like search, insert, and delete. Specialized trees like Red-Black Trees or AVL trees balance themselves during these operations. But what if you're handed an unbalanced tree to start with?

The Significance of Using an Array

Arrays are a versatile data structure and can be incredibly efficient when it comes to sorting and retrieving data. In the context of balancing a BST, an array serves as a temporary holding place for the tree's elements, sorted in ascending order. Once we have this sorted array, creating a balanced tree becomes a straightforward task.

How We Arrive at This Strategy

Balancing a tree involves ensuring that the left and right subtrees of each node differ in height by at most one. A sorted array inherently satisfies this constraint when converted back into a BST, making it an excellent strategy for our purpose.

The Two-Step Algorithm: Insight and Intuition

Here are the two key steps, along with the intuition behind them:

Step 1: In-Order Traversal into an Array

• What We Do: Perform an in-order traversal of the given unbalanced BST and store each node's value in an array.
• Why We Do It: An in-order traversal of a BST naturally produces a sorted list of its elements. This array now contains all elements of the BST in their proper order but without the baggage of the tree's previous imbalances.

Step 2: Create a Balanced BST from the Sorted Array

• What We Do: Recursively pick the middle element from the sorted array to be the root and repeat the process for the sub-arrays to form left and right subtrees.
• Why We Do It: Choosing the middle element ensures that the tree remains balanced. The left and right halves of the array naturally form the left and right subtrees of each node, maintaining the balanced property.

If you're looking to balance an existing Binary Search Tree (BST), you're in luck. We have a straightforward two-step plan to get you there, leveraging the power of arrays and recursion.

Step 1: The Array

In-Order Traversal: A Journey Through the Tree

In this step, we'll be doing an in-order traversal of the BST and store the nodes in an array. This array will serve as the foundation for building a balanced BST.

• C++ STL’s Vector: In C++, we use the vector data structure from the Standard Template Library (STL) for dynamic array handling.

• Python’s List: In Python, we use the built-in list data structure.

Here, we create a convenience function to do the in-order traversal and store the nodes in an array.

1# Convenience function for creating an array from BST in-order traversal
2def create_array_from_tree(root, arr):
3    if not root: return arr
4
5    arr = create_array_from_tree(root.left, arr)
6    arr.append(root.val)
7    arr = create_array_from_tree(root.right, arr)
8
9    return arr

Step 2: Crafting the Balanced BST

Breaking Down the Pseudocode

Let’s delve into the pseudocode that describes how we can create a balanced BST from a sorted array. The elegance here is in the recursive nature of the problem and the solution.

Base Case: The Simplest Scenario

1. When the Array is Empty: If the array has no elements, return a null pointer.

Recursive Case: Where the Magic Happens

0. Define a Build Method: This is where you'll craft the balanced tree.
1. Find the Middle: Take the middle element of the array and create a root node with it.
2. Craft the Left Subtree: Call build recursively on the left half of the array. The returned pointer becomes the left child of the root.
3. Craft the Right Subtree: Similarly, call build recursively on the right half. The returned pointer becomes the right child of the root.
4. Return the Root: Finally, return the pointer to the root node you created.

Finding the Middle: The Formula

To find the middle of the array, use the formula (size/2). This assumes a zero-based index, typical in most programming languages.

Let's look at some examples to see how the previous pseudo code works. We'll take a few simple scenarios and then build a more complex one.

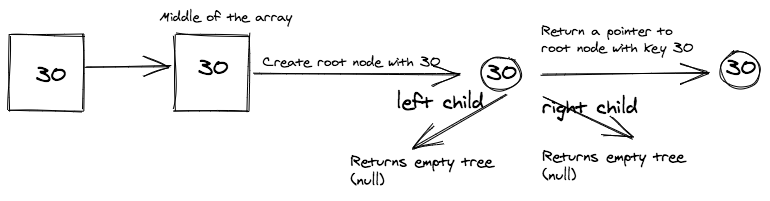
Array: [30]

First we look at the following array with just one element (i.e. 30).

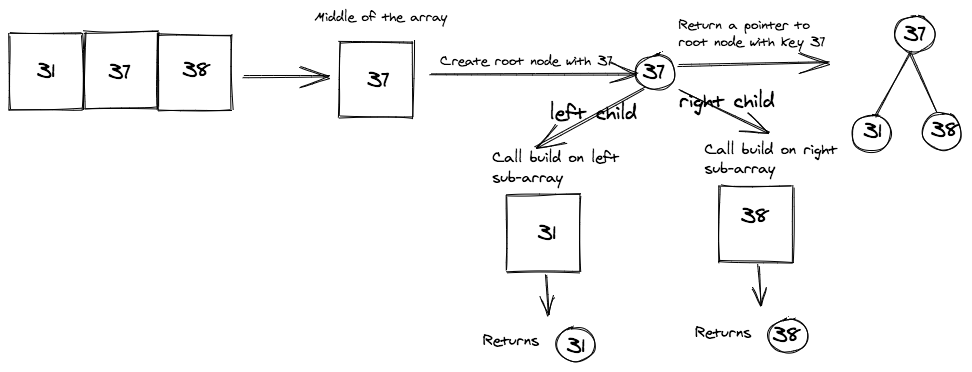
Array: [31, 37, 38]

Now let's look at an array of size 3.

Array: [10, 11]

Let us now go for an even sized array with two elements.

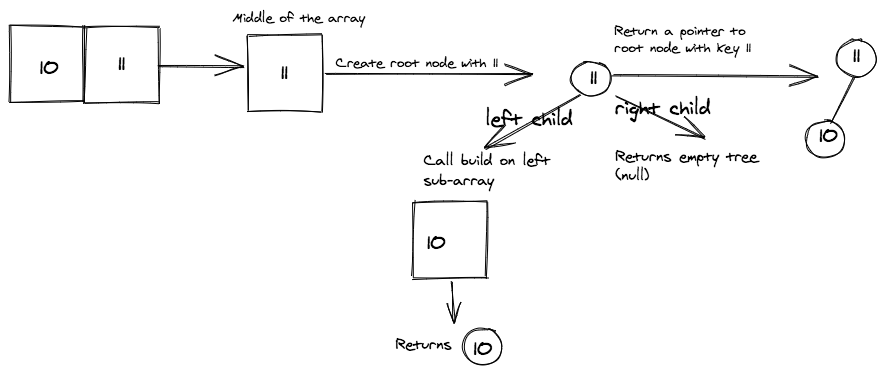
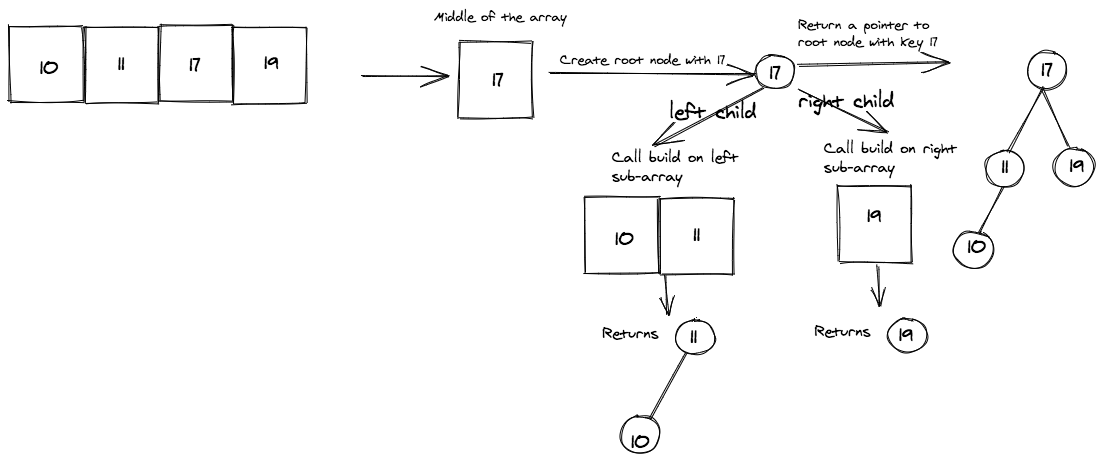
Array: [10, 11, 17, 19]

We can now extend the example to an even sized array with four elements.

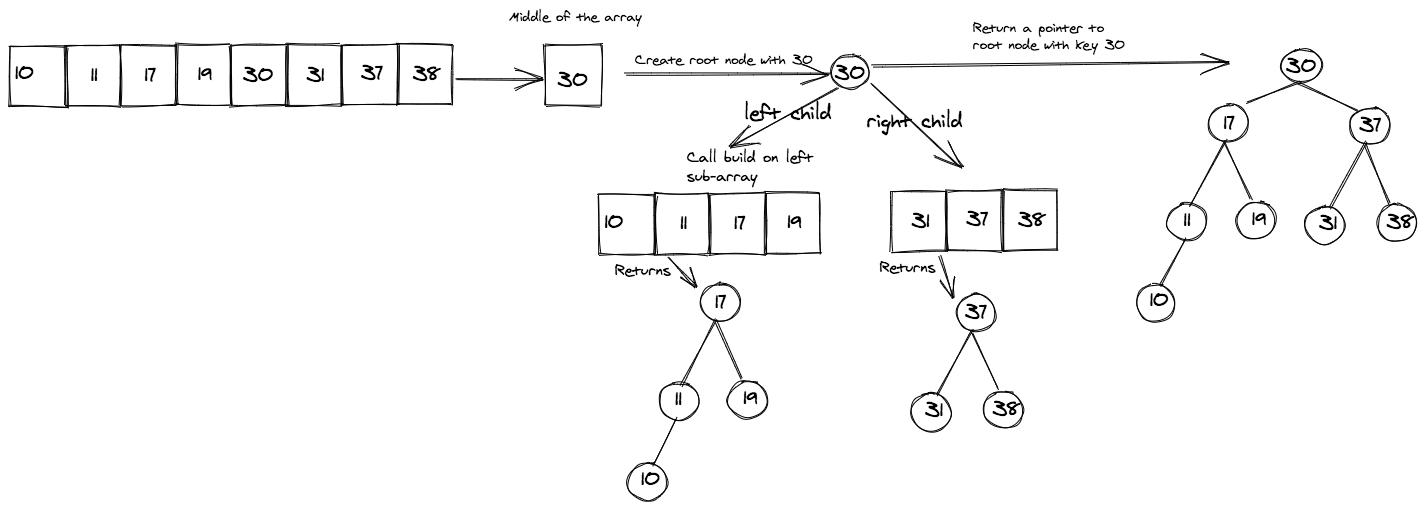
Array: [10, 11, 17, 19, 30, 31, 37, 38]

An even sized array with eight elements.

Before trying out the above code, it is always best to sit down with a paper and pen and conduct a dry run of the code a few times to see how it works.

Complexity of the Algorithm

The previous code has a complexity of O(N), where N is the number of nodes in the tree.

Inorder traversal requires O(N) time. As we are accessing each element of the array exactly once. After that, we are calculating the median value of the array, breaking it into two halves, and again calculating the median. This will take O(logN) time. Finally, the build method also has a time complexity of O(N).

So the total time complexity would be O(N+logN+N) ~ O(N).

We are creating an array of size N. And then again creating a binary tree of size N. And also, keep in mind that this is a recursive call that is called twice with half the data of the first call. So it will take a memory of O(logN).

So the total memory complexity would be O(N+N+logN) ~ O(N) as well.

One Pager Cheat Sheet

• A binary tree is a recursive structure composed of one Node with a key value and up to two child Nodes that can be traversed with a root pointer.
• A BST is a special type of binary tree where the key values are placed according to a defined rule; nodes in the left subtree have keys less than the parent, and keys in the right subtree have keys greater than the parent.
• Every node in a binary search tree at most has two children and duplicates can be added, but must be placed in the same subtree.
• A balanced BST is a Binary Search Tree in which the left and right subtrees differ in height by no more than 1.
• A binary tree can be rebalanced to become a balanced BST, thereby ensuring that all subtrees of a given node will differ in height by no more than one (1).
• Create a balanced BST tree from a sorted array based on the in-order traversal of the unbalanced tree for efficient balancing.
• We are creating an array from BST in-order traversal using a vector and also recursively creating a balanced BST using build method with the middle array element being the root node.
• We are building a balanced binary tree from arrays of different lengths to view the pseudo code in action.
• We can start balancing our BST by coding the build function, with 0 and n-1 as its starting and ending parameters, respectively.
• Before trying out the code, it is best to conduct a dry run to get an idea of the time and memory complexities (which are O(N)) of the inorder traversal algorithm.
• It is possible to convert an array into a balanced Binary Search Tree (BST) using inorder traversal to divide the array and create a root node and subtrees that differ in height by one.
• It is not possible to convert a BST to a balanced BST without using recursion, as there is no algorithm known to have a better time complexity than O(n log n).