Kruskal's Algorithm: A Hands-On Guide with Visuals

Ready to dig into Kruskal's Algorithm? Let's break it down, from the big picture to the nitty-gritty, with code snippets and ASCII diagrams to help visualize each step.

Quick Recap: The Three Pillars of Kruskal's Algorithm

Core Principles

• Empty Canvas: Start with no edges, just vertices.
• Bargain Hunt: Add edges by ascending weight.
• No Loops: Avoid cycles.

Why It Works

• Strategy: Greedy approach—grab the cheapest edge.
• Outcome: A Minimum Spanning Tree (MST) without cycles.

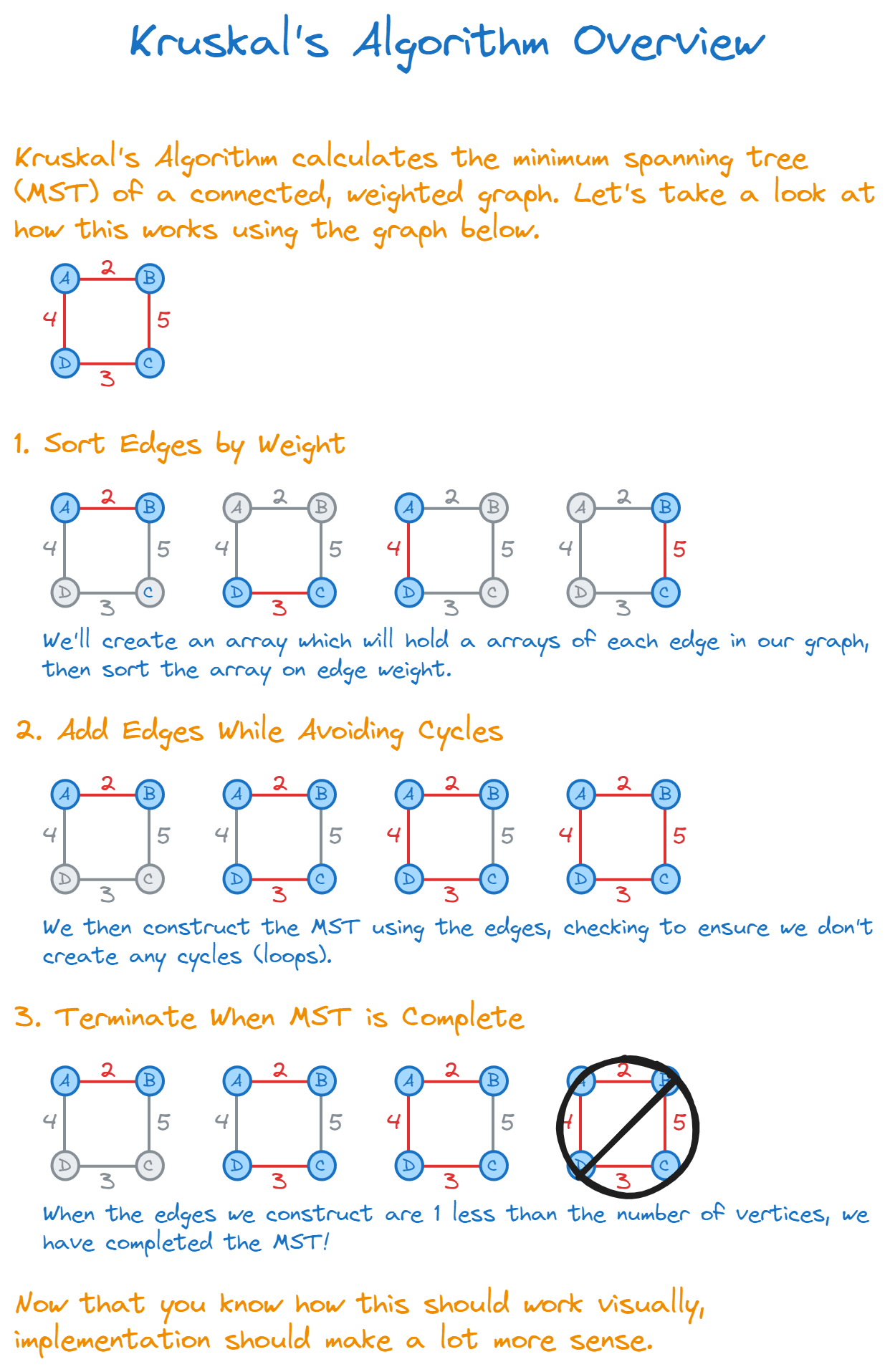
Step-By-Step: Building the MST

Let's use a sample graph for this walkthrough. Here's our original graph:

1  A--2--B
2  |     |
3  4     5
4  |     |
5  D--3--C

1. Sort Edges by Weight

First, list edges in ascending order by weight.

1let edges = [['2', 'A', 'B'], ['3', 'C', 'D'], ['4', 'A', 'D'], ['5', 'B', 'C']];
2edges.sort();

2. Add Edges While Avoiding Cycles

Go through the sorted list and add edges to the MST, skipping any that would create a cycle.

1let mst = new Set();
2
3// For each edge in sorted list
4for (let edge of edges) {
5    let weight = edge.weight;
6    let u = edge.u;
7    let v = edge.v;
8    // Check for cycle and add if safe
9}

For example:

• Add edge A-B (weight 2). MST becomes:

1  A--B

• Next, add edge C-D (weight 3). MST becomes:

1  A--B
2  
3  C--D

• Add A-D: This edge will connect the two separate trees and does not form a cycle.

1  A--B
2  |
3  D--C

• Skip B-C: This would create a cycle, so it's skipped.

3. Terminate When MST is Complete

Stop once the MST has ( V - 1 ) edges.

1if (mst.length === vertices.length - 1) {
2    break;
3}

MST In Action: Seeing the Pieces Come Together

As you add each edge, the MST takes shape:

• After adding A-B:

  TEXT

  1A--B

• After adding C-D:

  TEXT

  1A--B
  2
  3C--D

• After adding B-C:

  TEXT

  1A--B
  2|
  3D--C

With these steps, you've built an MST from scratch.