AlgoDaily - Contiguous Subarray Sum

Good afternoon! Here's our prompt for today.

Given an array of numbers, return true if there is a subarray that sums up to a certain number n.

A subarray is a contiguous subset of the array. For example the subarray of [1,2,3,4,5] is [1,2,3] or [3,4,5] or [2,3,4] etc.

JAVASCRIPT

1const arr = [1, 2, 3], sum = 5
2subarraySum(arr, sum)
3// true
4// [2, 3] sum up to 5
5
6const arr = [11, 21, 4], sum = 9
7subarraySum(arr, sum)
8// false
9// no subarrays sums up to 9

In the above examples, [2, 3] sum up to 5 so we return true. On the other hand, no subarray in [11, 21, 4] can sum up to 9.

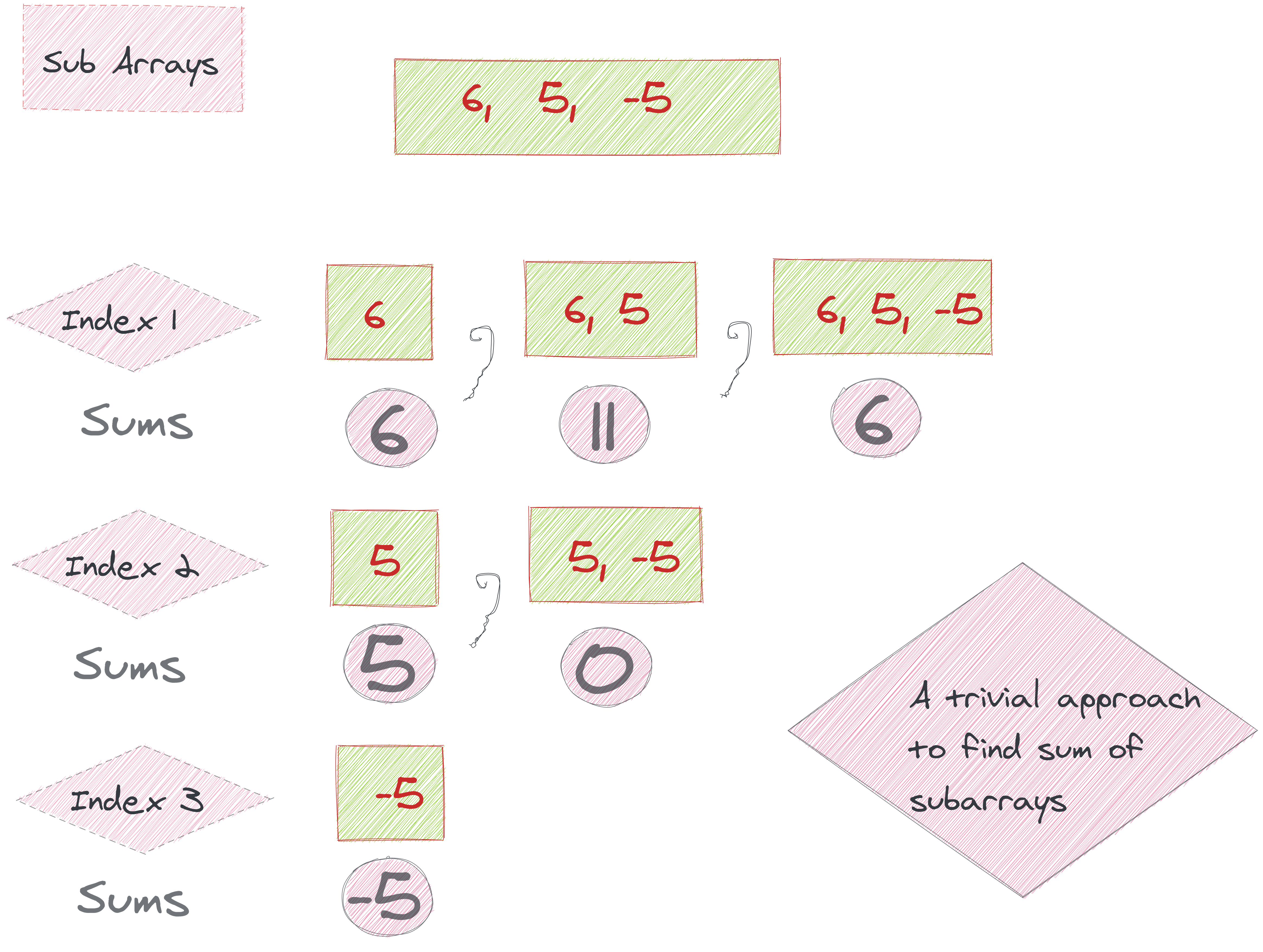
Can you create a function subarraySum that accomplishes this?

Constraints

Length of the array <= 100000
The values in the array will be between 0 and 1000000000
The target sum n will be between 0 and 1000000000
The array can be empty
Expected time complexity : O(n)
Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
var assert = require('assert');
​
function subarraySum(nums, n) {
  // hash of prefix sums
​
  // Fill in this method
  return nums;
}
​
const arr = [1, 2, 3],
  sum = 5;
console.log(subarraySum(arr, sum));
​
try {
  assert.equal(subarraySum([1, 2, 3], 3), true);
​
  console.log('PASSED: ' + 'assert.equal(subarraySum([ 1, 2, 3 ], 3), true)');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(subarraySum([], 3), false);
​
  console.log('PASSED: ' + 'assert.equal(subarraySum([], 3), false)');
} catch (err) {
  console.log(err);
}
​

Tired of reading? Watch this video explanation!

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

We'll now take you through what you need to know.

How do I use this guide?

Let's take another example. If the input was [3, 2, 5, 1] and our target number was 6, we'd witness the following if we did tried the brute force solution by hand:

xxxxxxxxxx
 
// the left side are the subsets we're trying
​
3 & 2        // curr_sum is 5, < 6, continue
3 & 2 & 5    // too big, skip
2 & 5        // curr_sum is 7, skip
5 & 1        // match!

With arrays, we can iteratively generate and run through every subarray within the array. Thus, the easiest brute force solution may be to simply test every subarray sum against n.

xxxxxxxxxx
 
function subarraySum(nums, sum) {
  let currSum, i, j;
  for (i = 0; i < nums.length; i += 1) {
    currSum = nums[i];
    j = i + 1;
    while (j <= nums.length) {
      if (currSum == sum) {
        return true;
      }
      if (currSum > sum || j == nums) {
        break;
      }
      currSum = currSum + nums[j];
      j += 1;
    }
  }
  return false;
}
​
console.log(subarraySum([1, 2, 3], 5));

Build your intuition. Click the correct answer from the options.

Which of these could be a valid brute force solution?

Click the option that best answers the question.

Recursively split the array in half
Iterate through and sum
Try every subarray sum
Use a linked list

We Can Do Better

The above code will complete a scan of every subarray possible. It does so by iterating through every element in the array. Then, at each loop, it tests every subarray with that starting index.

This works but is wildly inefficient. What if there were millions or billions of elements in each array? This caveat can also be understood by the time complexity of the brute force approach. As we are iterative through the array for each given n elements, the time complexity is O(n^2). So for a million elements in the array, there will be 10^12 operations which is huge. Perhaps we don't need to test each possible subarray -- so what if we didn't?

To make the brute force more efficient, we will be using a very popular data structure named: Hash Table.

A hash table keeps a key-value pair in a table using a hash function. As the hash function directly returns the memory address of the value given a key, its search, insert, and delete operations are in constant O(1) time.

We will be using a hash table to store the cumulative sum of the array as a key and its ending elements index as the value.

Try this exercise. Is this statement true or false?

A hash table supports the search, insert, and delete operations in constant O(1) time.

Press true if you believe the statement is correct, or false otherwise.

Build your intuition. Is this statement true or false?

We can only find a contiguous subarray summing to a certain number in O(n^2) time complexity or greater.

Press true if you believe the statement is correct, or false otherwise.

Try this exercise. Could you figure out the right sequence for this list?

What could be the right order for the contiguous subarray sum algorithm?

Press the below buttons in the order in which they should occur. Click on them again to un-select.

Options:

Otherwise, store the sum as a key in the hash
At each step, calculate the running sum
Iterate through the array
Try to find the difference of the running sum and the target in the hash

Notice that most of the subarrays overlap in some way. In [3, 2, 5, 1], [3, 2] is part of [3, 2, 5]. It seems there's an opportunity to keep track of just one thing for now.

The final solution has us using a hash map/dict to store previous subarray sums.

One Pager Cheat Sheet

Create a function subarraySum that returns true if a contiguous subarray sums up to a certain number n with a time complexity of O(n) and a space complexity of O(n).
By brute force, we can manually check possible combinations of elements from the array [3, 2, 5, 1] to identify if they add up to the target number of 6.
We can iteratively test every subarray of the array to find the brute force solution to the problem.
A brute force solution involves exhaustively searching through all possible solutions to find the desired result.
We can do better than O(n^2) time complexity by avoiding testing each possible subarray.
We will be using a Hash Table to store the cumulative sum of the array as a key and its ending elements index as the value in order to improve the efficiency of the brute force algorithm.
A hash table uses a hash function to store the key-value pairs in a table, enabling search, insert, and delete operations to be executed in constant O(1) time.
A hash table enables constant time operations for search, insert, and delete, whereas finding a contiguous subarray summing to a certain number requires O(n^2) or greater time complexity due to the need for a brute-force approach involving iterating through all possible subarrays.
We can calculate and store the running sum in a hash, allowing us to check if a subarray sum matches the target in O(n^2) time complexity or greater.
We can use a hash map to store previous subarray sums and track only one thing, since most subarrays overlap in some way.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function subarraySum(nums, n) {
  let sumsMap = { 0: 1 }; // hash of prefix sums
  let sum = 0;
  for (let num of nums) {
    sum += num; // increment current sum
    if (sumsMap[sum - n]) {
      return true;
    }
    // store sum so far in hash with truthy value
    sumsMap[sum] = true;
  }
  return false;
}
​
const arr = [1, 2, 3],
  sum = 5;
console.log(subarraySum(arr, sum));
​
try {
  assert.equal(subarraySum([1, 2, 3], 3), true);
​
  console.log('PASSED: ' + 'assert.equal(subarraySum([ 1, 2, 3 ], 3), true)');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(subarraySum([], 3), false);
​
  console.log('PASSED: ' + 'assert.equal(subarraySum([], 3), false)');

Great job getting through this. Let's move on.

If you had any problems with this tutorial, check out the main forum thread here.