AlgoDaily - Zeros to the End

Good afternoon! Here's our prompt for today.

Write a method that moves all zeros in an array to its end. You should maintain the order of all other elements. Here's an example:

JAVASCRIPT

1zerosToEnd([1, 0, 2, 0, 4, 0])
2// [1, 2, 4, 0, 0, 0]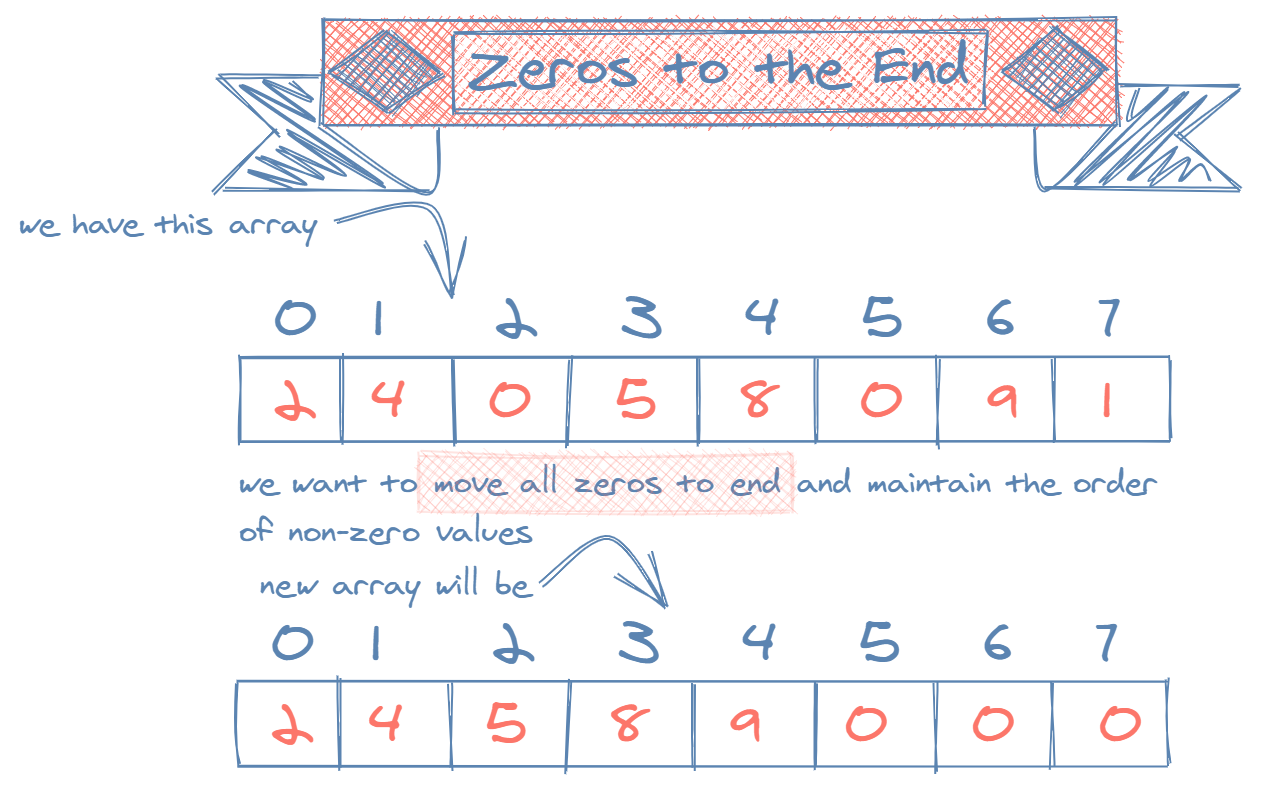

Here's another one:

JAVASCRIPT

1zerosToEnd([1, 0, 2, 0, 4, 0])
2// [1, 2, 4, 0, 0, 0]

Fill in the following function signature:

JAVASCRIPT

1function zerosToEnd(nums) {
2  return;
3};

Can you do this without instantiating a new array?

Constraints

Length of the array <= 100000
The array will always contain integer values between -1000000000 and 1000000000
Expected time complexity : O(n)
Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
var assert = require('assert');
​
function zerosToEnd(nums) {
  // Fill in this method
  return nums;
}
​
console.log(zerosToEnd([1, 0, 2, 0, 4, 0]));
​
try {
  assert.deepEqual(zerosToEnd([1, 0, 2, 0, 4, 0]), [1, 2, 4, 0, 0, 0]);
​
  console.log(
    'PASSED: `zerosToEnd([1, 0, 2, 0, 4, 0])` should get us `[1, 2, 4, 0, 0, 0]`'
  );
} catch (err) {
  console.log(err);
}
​
try {
  assert.deepEqual(
    zerosToEnd([4, 13, 0, 2, 0, 0, 15, 0]),
    [4, 13, 2, 15, 0, 0, 0, 0]
  );
​
  console.log(
    'PASSED: `zerosToEnd([4, 13, 0, 2, 0, 0, 15, 0])` should get us `[4, 13, 2, 15, 0, 0, 0, 0]`'
  );
} catch (err) {

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's how we would solve this problem...

How do I use this guide?

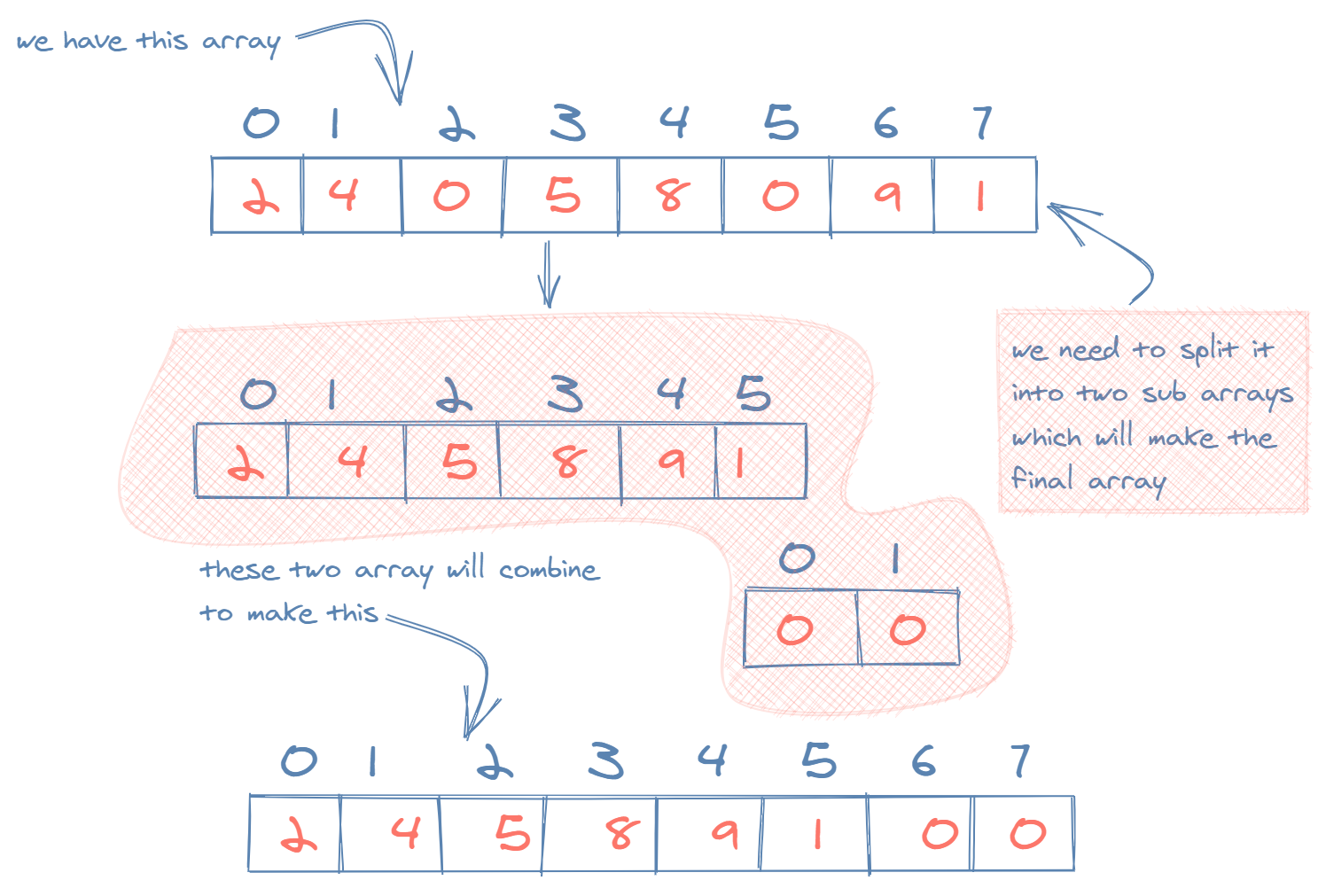
Always start by running through some examples to get a feel for the problem. With [1, 0, 2, 0, 4, 0], let's walk through the steps-- in this case, it may be best to work backwards.

We want to end up with [1, 2, 4, 0, 0, 0]. To do that, it seems like we need to separate out [1, 2, 4] and [0, 0, 0], so there's 3 things to consider.

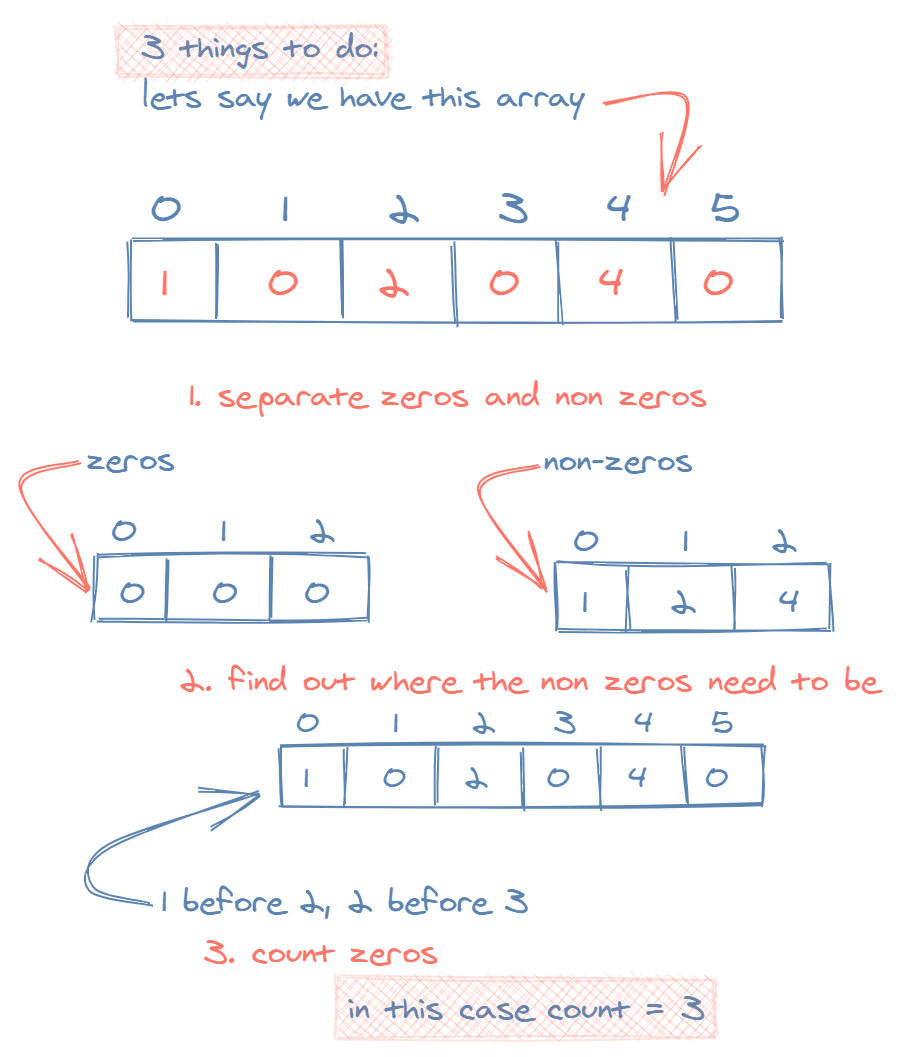
We need to do these 3 things:

Separate the 0s and non-0s.
Find out where the non-0s need to be index-wise
Keeping track of the number of 0s

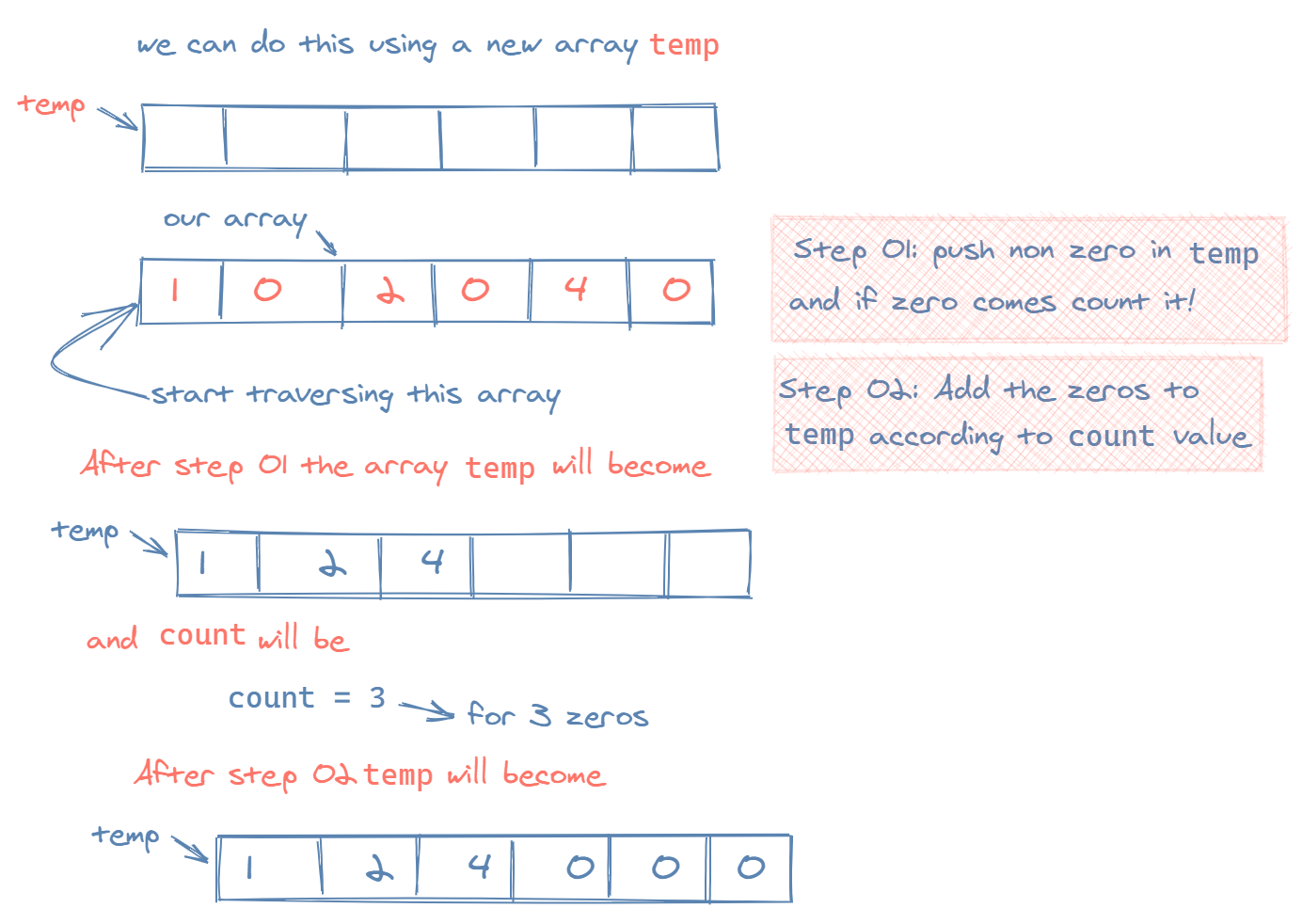
We have a potential brute force solution! This could be our pseudocode.

xxxxxxxxxx
 
temp = []
zero_count = 0
iterate through array:
  if nonzero, push to new temp
  if zero, increment count
for zero_count times:
  push to temp
return temp

We can do better.

The above snippet would get the job done, but requires extra space with the new temp array.

Without a temp array, we'll need to change the position of elements in the array in-place. This means that we'll need to mutate the array's elements directly. This requires us to keep track of indexes.

xxxxxxxxxx
 
const arr = [1, 0, 2, 0, 4, 0];
const nonZeros = [1, 2, 4]

Here's a thought exercise.

Perhaps we can try to simplify-- what if we just kept track of one index?

Then, what if we used multiple trackers? Would it be beneficial to know about multiple positions at once, in the context of this problem?

Multiple pointers is key.

Because we don't need or care about what is in the array after non-zero elements, we can simply keep a separate pointer of where to start the zeros. This extra pointer will prevent us from having to store a separate temp array, with the intuition being that we know what we need to fill after (exclusively 0s!).

Despite having two loops, the time complexity simplifies to O(n). However, the space complexity is constant since we're using the same array.

Follow the below illustration for more guidance:

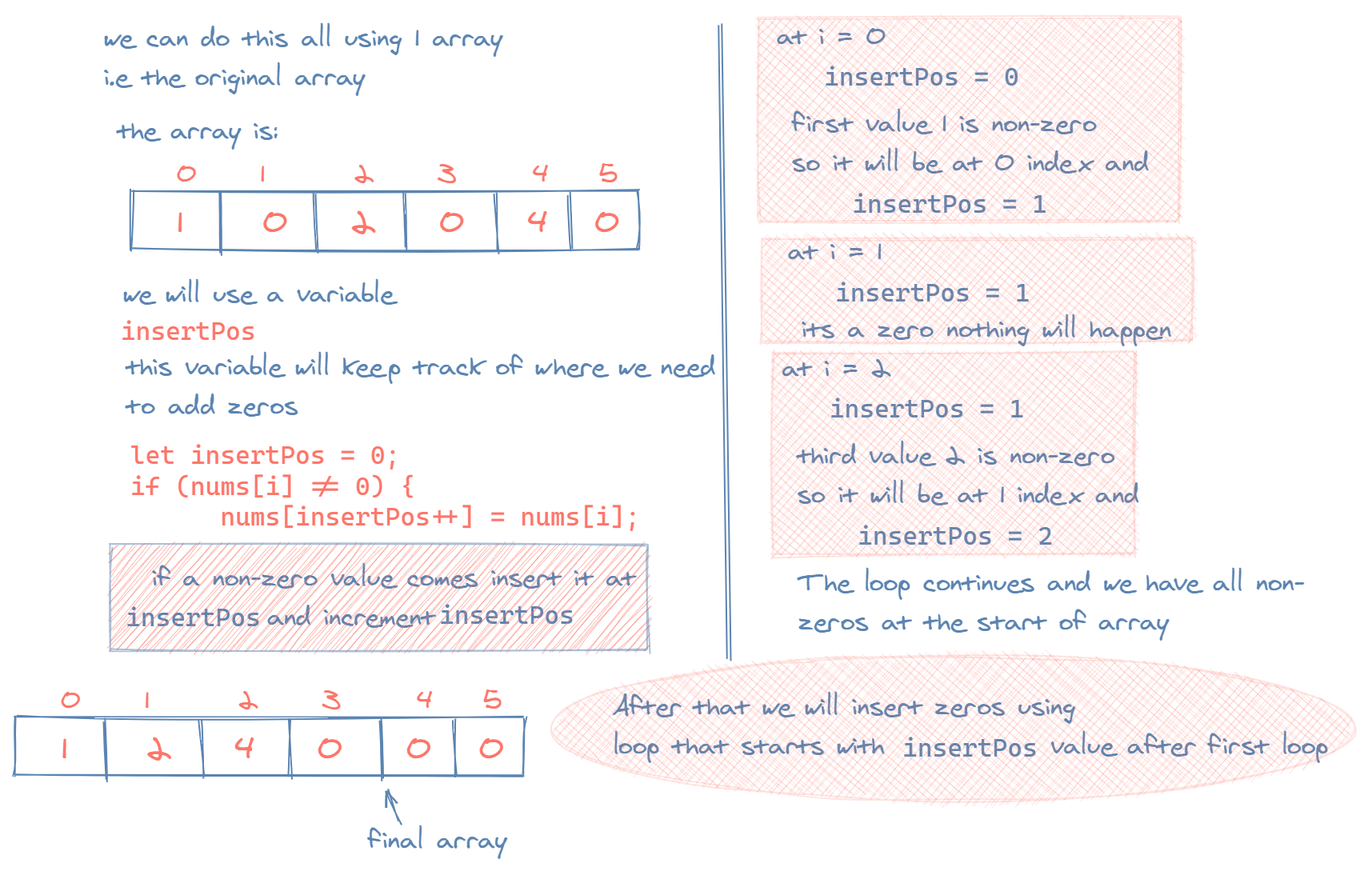
One Pager Cheat Sheet

Write a function zerosToEnd which moves all zeros in an array to its end, while maintaining the order of all other elements, within O(n) time and O(1) space complexity constraints.
Run through examples and separate the [1, 2, 4] from the [0, 0, 0] to achieve [1, 2, 4, 0, 0, 0].
We need to separate the 0s and non-0s, find out where the non-0s need to be index-wise, and keep track of the number of 0s in order to solve this problem using a potential brute force solution.
We can do better by changing the position of elements in the array in-place, which requires us to mutate and keep track of indexes.
Try simplifying the problem by only keeping track of one index, or use multiple trackers to know about multiple positions at once.
Multiple pointers are key for efficiently moving all zeros to the end of an array in O(n) time complexity and constant space complexity.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function zerosToEnd(nums) {
  let insertPos = 0;
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] != 0) {
      nums[insertPos++] = nums[i];
    }
  }
​
  for (let j = insertPos; j < nums.length; j++) {
    nums[j] = 0;
  }
​
  return nums;
}
​
console.log(zerosToEnd([1, 0, 2, 0, 4, 0]));
​
try {
  assert.deepEqual(zerosToEnd([1, 0, 2, 0, 4, 0]), [1, 2, 4, 0, 0, 0]);
​
  console.log(
    'PASSED: `zerosToEnd([1, 0, 2, 0, 4, 0])` should get us `[1, 2, 4, 0, 0, 0]`'
  );
} catch (err) {
  console.log(err);
}
​
try {
  assert.deepEqual(
    zerosToEnd([4, 13, 0, 2, 0, 0, 15, 0]),

You're doing a wonderful job. Keep going!

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Here's a video of us explaining the solution.

Here's how we would solve this problem...

We can do better.

Multiple pointers is key.

One Pager Cheat Sheet

This is our final solution.

You're doing a wonderful job. Keep going!

Programming Categories

Popular Lessons