Kruskal's Algorithm: Your Coding Interview Compass for Navigating Minimum Spanning Trees

Welcome to the fascinating realm of graph algorithms! Today, we're diving into Kruskal's Algorithm—a topic that often surfaces in coding interviews. Why? Because it's like a Swiss Army knife for showcasing your mastery of computer science basics.

Introduction: Why Kruskal's Algorithm?

Your Ticket to a Minimum Spanning Tree

Imagine you're an architect, and you need to build a network of roads that connects several cities but with the minimum amount of asphalt. Kruskal's algorithm helps you do just that, but for graphs!

• How: It calculates the minimum spanning tree (MST) of a connected, weighted graph.
• Why: The MST is the subset of edges that connects all vertices with the smallest total weight.

A Coding Interview Goldmine

Picture Kruskal's algorithm as a multi-level video game that tests various skills.

• How: Implementing it involves grappling with graphs, greedy algorithms, union-find data structures, and time complexity.
• Why: Navigating through these challenges proves you're well-versed in fundamental computer science concepts, making you a desirable candidate.

Background: Setting the Stage

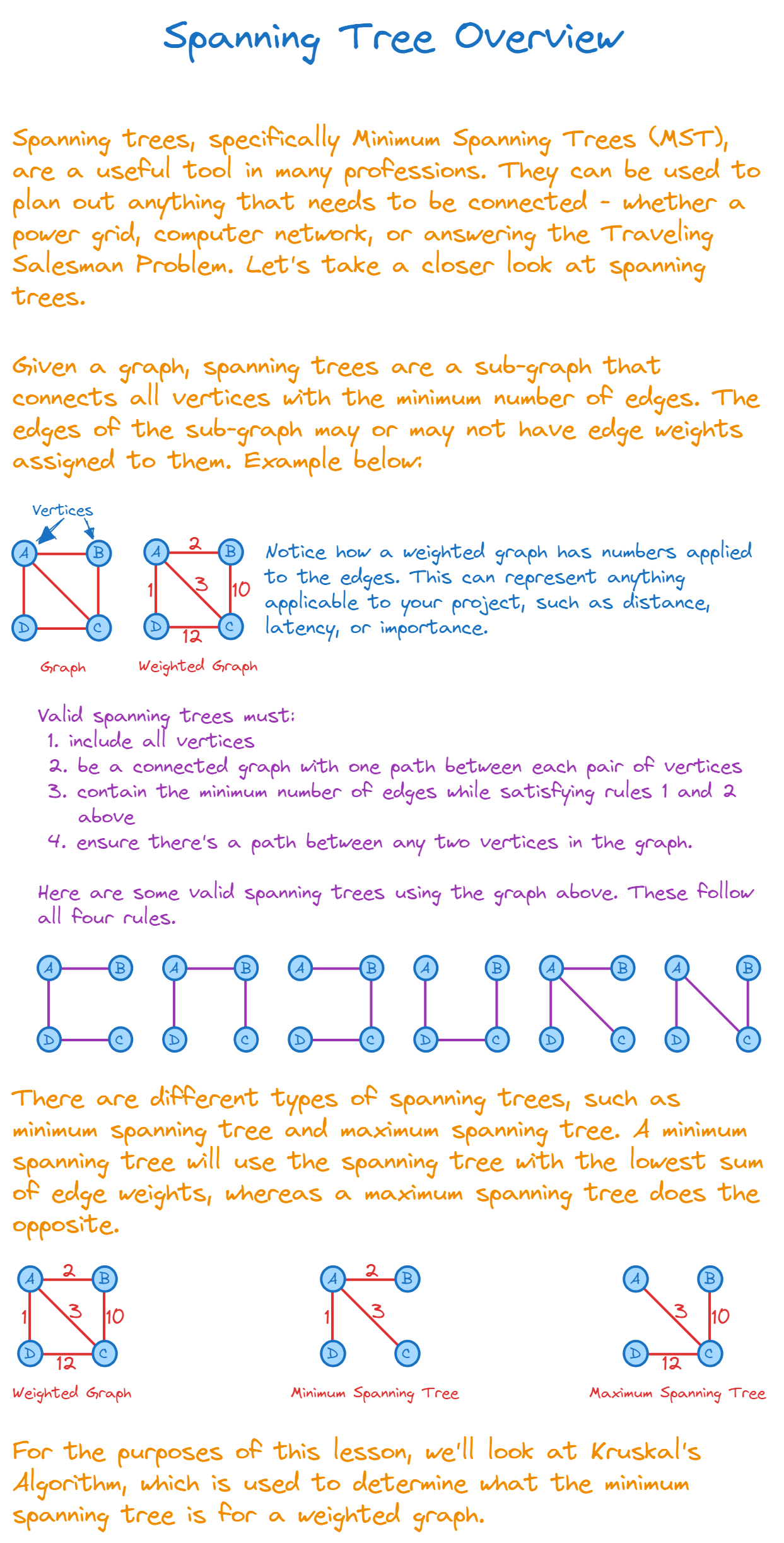
What is a Minimum Spanning Tree?

Think of an MST as a power grid that connects all houses in a neighborhood with the least amount of wire.

• How: An MST is a tree extracted from a connected, weighted graph, where the sum of edge weights is minimized.
• Why: It ensures all vertices are connected without any cycles, optimizing the total cost.

The Real-World Magic of MSTs

Imagine you're tasked with laying down internet cables across a city or designing a circuit board. Here's where MSTs come to the rescue!

• How: MSTs have a wide range of applications in networks, circuit design, and facility location.
• Why: They allow you to connect various nodes (like cities or circuit components) while minimizing cost or resource usage.

So, ready to learn how to implement Kruskal's algorithm and ace your coding interviews? Let's roll up our sleeves and get started!

Kruskal's Algorithm: A Hands-On Guide with Visuals

Ready to dig into Kruskal's Algorithm? Let's break it down, from the big picture to the nitty-gritty, with code snippets and ASCII diagrams to help visualize each step.

Quick Recap: The Three Pillars of Kruskal's Algorithm

Core Principles

• Empty Canvas: Start with no edges, just vertices.
• Bargain Hunt: Add edges by ascending weight.
• No Loops: Avoid cycles.

Why It Works

• Strategy: Greedy approach—grab the cheapest edge.
• Outcome: A Minimum Spanning Tree (MST) without cycles.

Step-By-Step: Building the MST

Let's use a sample graph for this walkthrough. Here's our original graph:

1  A--2--B
2  |     |
3  4     5
4  |     |
5  D--3--C

1. Sort Edges by Weight

First, list edges in ascending order by weight.

1type Edge struct {
2    weight int
3    start, end string
4}
5edges := []Edge{{2, "A", "B"}, {3, "C", "D"}, {4, "A", "D"}, {5, "B", "C"}}
6sort.Slice(edges, func(i, j int) bool {return edges[i].weight < edges[j].weight})

2. Add Edges While Avoiding Cycles

Go through the sorted list and add edges to the MST, skipping any that would create a cycle.

1mst := map[int]struct{}{}
2
3// For each edge in sorted list
4for _, edge := range edges {
5    weight := edge.Weight
6    u := edge.U
7    v := edge.V
8    // Check for cycle and add if safe
9}

For example:

• Add edge A-B (weight 2). MST becomes:

1  A--B

• Next, add edge C-D (weight 3). MST becomes:

1  A--B
2  
3  C--D

• Add A-D: This edge will connect the two separate trees and does not form a cycle.

1  A--B
2  |
3  D--C

• Skip B-C: This would create a cycle, so it's skipped.

3. Terminate When MST is Complete

Stop once the MST has ( V - 1 ) edges.

1if len(mst) == len(vertices) - 1 {
2    break
3}

MST In Action: Seeing the Pieces Come Together

As you add each edge, the MST takes shape:

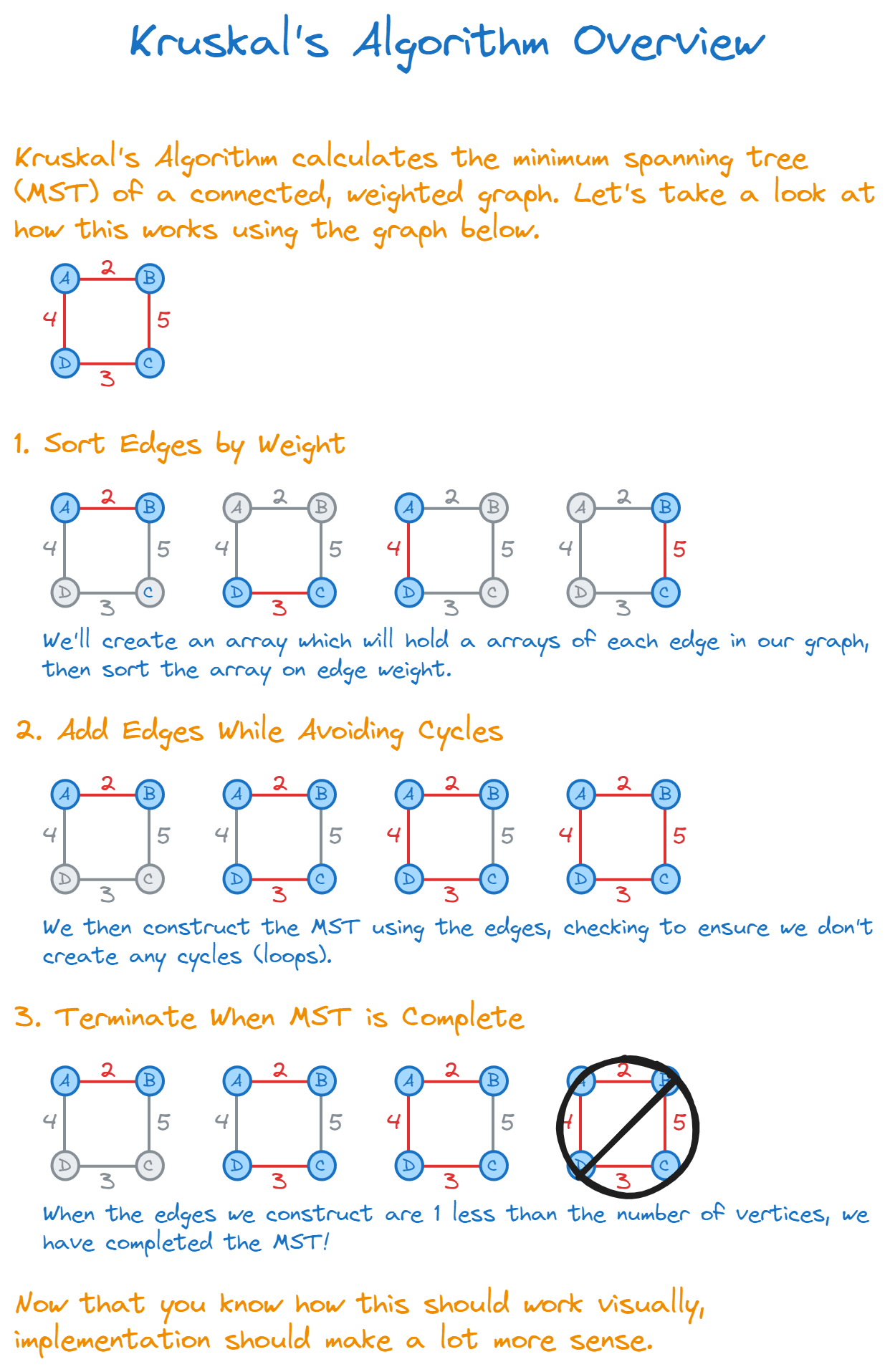
• After adding A-B:

  TEXT

  1A--B

• After adding C-D:

  TEXT

  1A--B
  2
  3C--D

• After adding B-C:

  TEXT

  1A--B
  2|
  3D--C

With these steps, you've built an MST from scratch.

Implementing Kruskal's Algorithm: A Practical Guide

Let's start by discussing the major components you'll need.

Harness the Power of Union-Find

Think of the union-find data structure as a network of social circles, helping us keep track of connected components.

• How: Maintain disjoint sets to verify whether vertices are connected.
• Why: This enables us to quickly determine whether adding an edge will form a cycle.

1// Union-Find initialization
2parent := make(map[rune]rune)
3for _, vertex := range vertices {
4    parent[vertex] = vertex
5}
6
7func find(vertex rune) rune {
8    if parent[vertex] != vertex {
9        parent[vertex] = find(parent[vertex])
10    }
11    return parent[vertex]
12}
13
14func union(u, v rune) {
15    root_u := find(u)
16    root_v := find(v)
17
18    if root_u != root_v {
19        parent[root_u] = root_v
20    }
21}

Storing Edges: The Priority Queue Way

Imagine a priority queue as your shopping basket, always giving you the cheapest item first.

• How: Store edges in a priority queue, sorted by weight.
• Why: This ensures we always pick the edge with the lowest weight.

1import "container/heap"
2
3// Edge is a struct of an edge
4type Edge struct {
5	u, v, weight int
6}
7
8// Priority Queue
9type PriorityQueue []*Edge
10
11// Set up functions for heap interface
12func (pq PriorityQueue) Len() int { return len(pq) }
13
14func (pq PriorityQueue) Less(i, j int) bool {
15	return pq[i].weight < pq[j].weight
16}
17
18func (pq PriorityQueue) Swap(i, j int) {
19	pq[i], pq[j] = pq[j], pq[i]
20}
21
22func (pq *PriorityQueue) Push(x interface{}) {
23	item := x.(*Edge)
24	*pq = append(*pq, item)
25}
26
27func (pq *PriorityQueue) Pop() interface{} {
28	old := *pq
29	n := len(old)
30	item := old[n-1]
31	old[n-1] = nil  // avoid memory leak
32	*pq = old[0 : n-1]
33	return item
34}
35
36// Initialize the priority queue with edges
37var pq PriorityQueue
38heap.Init(&pq)
39for _, edge := range edges {
40	heap.Push(&pq, edge)
41}

The Edge-Adding Logic

It's like solving a puzzle; you only fit in the pieces that don't disrupt the existing picture.

• How: Check if adding an edge connects two different trees in the forest of disjoint sets.
• Why: This prevents cycles while ensuring connectivity.

1mst := make(map[Edge]struct{})
2
3for len(priorityQueue) > 0 {
4    edge := heap.Pop(&priorityQueue).(Edge)
5    weight := edge.weight
6    u := edge.u
7    v := edge.v
8
9    if find(u) != find(v) {
10        mst[Edge{u, v, weight}] = struct{}{}
11        union(u, v)
12    }
13}

Optimizing the Algorithm: Performance Tweaks

Using Union by Rank

Think of union by rank as a merger between companies, where the smaller company gets absorbed into the larger one.

• How: Maintain a rank variable for each set to make the union operation faster.
• Why: This keeps the tree balanced, reducing the time complexity.

Time Complexity: How Fast is Fast?

• How: The algorithm's time complexity is $O\left(E\log E\right)$.
• Why: Sorting edges takes $O\left(E\log E\right)$ and with optimized union-find, checking for cycles is $O\left(\log E\right)$ per operation.

Kruskal's Algorithm Complexity Analysis

Time Complexity

• $O\left(E\log E\right)$: Dominated by sorting edges and union-find operations.

Space Complexity

• $O\left(V\right)$: Mainly for storing the parent pointers in the union-find data structure.

Pros, Cons, and Alternatives: The Final Verdict

Pros: The Good Stuff

• Conceptually Simple: The algorithm is intuitive and provides an optimal solution.

Cons: The Not-So-Good

• Potentially Slow: If you sort all edges upfront, it could be a bottleneck.

Alternatives: Meet the Cousins

• Prim's Algorithm: Another option for finding a Minimum Spanning Tree, with different trade-offs.

Conclusion

Implementing Kruskal's algorithm demonstrates core CS abilities like working with graphs, greedy algorithms, union-find structures, and analyzing time complexity. These fundamentals are at the heart of many technical interviews.

At a high level, Kruskal's works by processing edges from lowest to highest weight, adding them to the MST one-by-one, skipping any that form cycles. This greedy approach results in the overall minimum spanning tree.

Thank you for following along with this tutorial on Kruskal's algorithm.

One Pager Cheat Sheet

• Kruskal's Algorithm is a coding interview topic known for demonstrating mastery of computer science basics, as it calculates the minimum spanning tree (MST) of a connected, weighted graph, testing skills like understanding of graphs, greedy algorithms, union-find data structures, and time complexity; MSTs, which connect all vertices without cycles and minimize total cost, have applications in networks, circuit design, and facility location.
• In graph theory, a Minimum Spanning Tree (MST) is a subset of a graph's edges that connects all vertices without cycles and with the minimum total edge weight, accomplished by using a minimization principle and a greedy approach in algorithms like Kruskal's.
• Kruskal's Algorithm constructs a Minimum Spanning Tree (MST) without cycles by starting with an empty canvas, sorting edges by weight, adding edges that do not create a cycle, and terminating when the MST is complete (has V - 1 edges), with the process illustrated through ASCII diagrams and code snippets in multiple languages.
• The guide details the implementation of Kruskal's Algorithm using union-find and priority queue data structures to prevent cycles, ensure connectivity, and always select edges with the lowest weight, demonstrating the procedure in multiple programming languages. The algorithm's time complexity is O(E log E) due to sorting edges and checking for cycles, while its space complexity is O(V) for storing parent pointers, with an additional performance tweak option provided: union by rank which balances the tree and reduces time complexity. The pros include simplicity and optimality, while the cons suggest potential slowness, alongside an alternative: Prim's Algorithm.
• Implementing Kruskal's algorithm showcases essential computer science skills including working with graphs, using greedy algorithms and union-find structures, and analyzing time complexity, with the algorithm functioning by processing edges from lowest to highest weight to create the minimum spanning tree.