Genetic Algorithm (GA) is a nature-inspired algorithm that has extensively been used to solve optimization problems. It belongs to the branch of approximation algorithms because it does not guarantee to always find the exact optimal solution; however, it may find a near-optimal solution in a limited time. In this lesson, we will learn the basics of GA in terms of its source of inspiration, general structure, working, and implementation.
A little about optimization
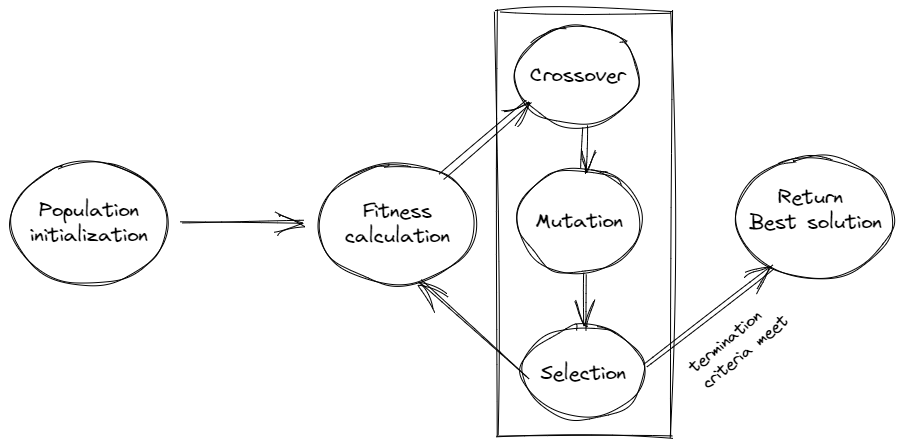
Optimization is the process of finding the best solution to a problem. For example, finding the shortest route to the destination, scheduling the hospital staff in the most efficient manner possible, or planning the day's activities to best utilize the available time. In order to solve the real-world optimization problems, the problems are formulated as mathematical functions and optimization deals with minimizing/maximizing the output of that function to find the best solution. Once the problem is formulated mathematically, an optimization algorithm such as GA is used to find the best solution (optimal solution) to that problem. The optimization process using GA is depicted in the following diagram.

Example
Let's say we have a function with two variables, x1 and x2, and we want to find the values of these variables that would allow the function to output the minimum value.
An optimization algorithm such as GA can be used to optimize the above function and find the optimal solution.
Genetic Algorithm (GA)
GA is an evolutionary algorithm and is inspired by the process of natural selection. According to Darwin, natural selection is a mechanism by which populations of different species adapt and evolve. The Fittest individuals survive and reproduce more similar offspring while weak individuals are eliminated with the passage of time. By taking inspiration from this concept, John Holland proposed GA in which a population of candidate solutions is generated randomly for a problem. Better solutions are given a higher chance to produce similar solutions by performing crossover. Obviously, a new generation will inherit more from better solutions resulting in the survival of the traits of better solutions.
Important terms and concepts
To better understand the structure and working of GA, it is required to first discuss a few important terms and concepts.
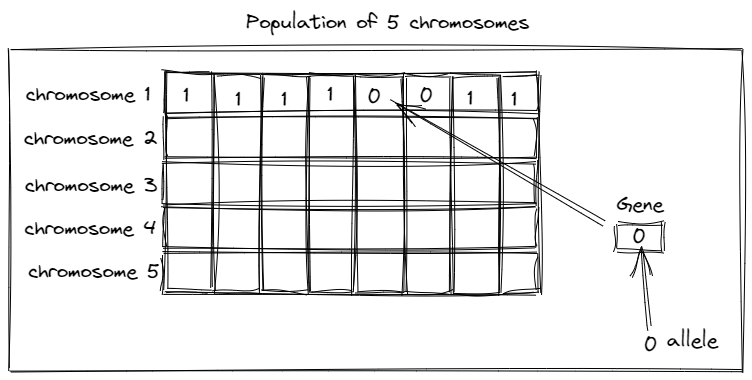
Chromosome
A chromosome is a candidate/potential solution to the problem being solved. The solution may not necessarily be the optimal solution. A chromosome may be considered as an array of binary/integer variables where each variable may be considered as a gene and the value of a variable is called an allele. For better understanding see the following diagram.
Population
A set of solutions participating in the process of optimization is called population. Unlike trajectory-based algorithms, GA is a population-based algorithm in which several solutions interact with each other to find the global optimum.
Objective function
It is also called a fitness function. Whenever an optimization problem is solved it is first formulated as a mathematical function that evaluates the quality/fitness of the candidate solution. We usually pass a solution to this function and this function returns the fitness of that solution. Once the fittest/optimal solution is found the process is stopped.
General structure and working of GA
GA mimics the process of natural selection that involves a few steps called genetic operators. First of all, a population of random solutions (chromosomes) is generated. The fitness of each candidate solution is calculated. After that, the genetic operators called crossover, mutation, and selection are performed in a sequence as shown in the following diagram.
Solution representation
A fundamental step is encoding or representing the solution. A solution/chromosome may be encoded as a binary string, integer-valued array, floating-point array, or a permutation of a fixed set of elements. For example:
• the solution of a feature selection problem may be encoded as a binary string where each gene will indicate whether a feature is selected or not;
• the solution of the following fitness function will be encoded as an integer array if x1 and x2 are discrete variables;
• the solution of the above fitness function will be encoded as a floating-point array if x1 and x2 are continuous variables;
• the solution of Travelling Salesman Problem (TSP) will be encoded as a set permutation;
Population initialization
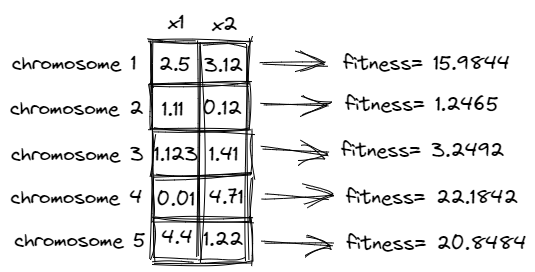
In GA and all other evolutionary algorithms, the population is usually generated randomly. For example, a randomly generated population of size 5 for the function mentioned in the previous subsection is depicted in the following diagram. We are assuming that x1 and x2 are continuous variables and both can have value in the range [-5, 5].
Fitness calculation
Each chromosome from the population is passed to the objective function one by one and its fitness is calculated. For example, the fitness of each of the randomly generated solutions in the previous step is calculated and depicted in the following figure.
Matting selection
In every iteration of GA, new solutions are generated from existing solutions. The operator that is used to produce new solutions from existing solutions is called crossover which is discussed in the next subsection. However, to perform crossover it is very important to select the most suitable solutions for crossover. A lot of methods have been proposed in the literature to select parents for crossover whereas each method has strengths as well as weaknesses. Two well-known selection methods are discussed below:
Selecting k best solutions
The simplest method is to first determine the pool size and then choose the best chromosomes based on the pool size. This pool is known as the matting pool, and parents are chosen from this pool to perform crossover in the next phase.
Fitness proportionate selection
In this method, each solution is assigned a probability of selection based on its fitness. A solution with better fitness, for example, will have a larger proportion on a scale of 0 to 1, resulting in a higher probability of being selected. The whole method is illustrated through the following diagram in which the fitness of each solution is divided by the sum of the fitness of all solutions. Then the accumulative probability distribution on the scale of 0 to 1 is calculated by summing the fitness of each solution into the sum of fitness of all previous solutions.

A random number in the range 0 to 1 will be generated and if it lies in 0 – 0.251 then chromosome 1 will be selected for crossover, if it lies in 0.252 – 0.2761 then chromosome 2 will be selected, and so on.
Build your intuition. Fill in the missing part by typing it in.
What would be the accumulative probability distribution for the following population on the scale of 0 to 1?
| X1 | X2 |
|---|---|
| 5 | 7 |
| 3 | 4 |
| 2 | 8 |
Write the missing line below.
Crossover operator
This is the reproduction phase which mimics the sexual reproduction mechanism of natural selection. The genetic information of two individuals called parents selected through matting selection is exchanged to produce new individuals called offspring. In the literature, many methods to perform crossover have been proposed; however, three well-known types are discussed in this subsection.
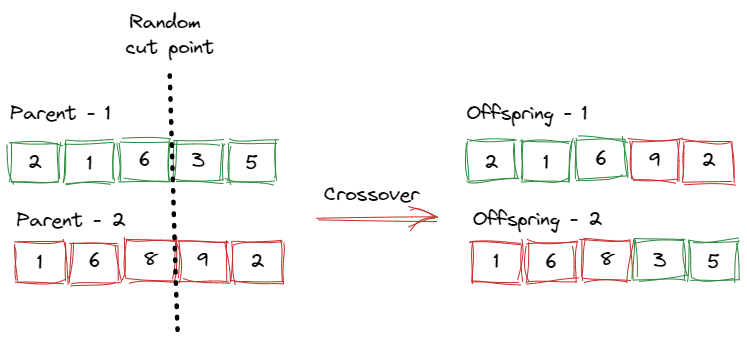
One-point crossover
In this crossover, one crossover point is chosen at random, and the first child is composed of the first half of parent-1 and the second half of parent-2, while the second child is made up of the first half of parent-2 and the second half of parent-1. It is shown in the following figure.
Multipoint crossover
We can generate multiple crossover points in this type of crossover, and offspring are generated by selecting alternative portions from both parents, as shown in the following diagram.

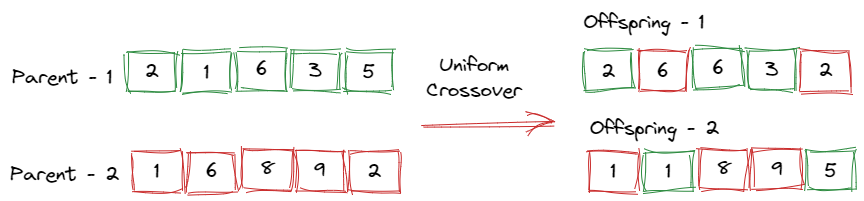
Uniform crossover
In this type of crossover, each gene for an offspring is selected with 0.5 probability from Parent-1 and 0.5 probability from Parent-2. If a gene from parent – 1 is selected, the same indexed gene from parent – 2 is chosen for the other offspring. It is demonstrated in the following diagram.
Mutation operator
Just like the crossover, this operator also mimics the biological mutation operator. Although, children inherit 99% of characteristics from their parent but mutation allows to introduce new traits in the genetic information of an individual. Moreover, it allows to maintain diversity and stops population converging prematurely. In the literature, there are so many ways to perform mutation; however, a few well-known techniques are discussed here in this lesson.
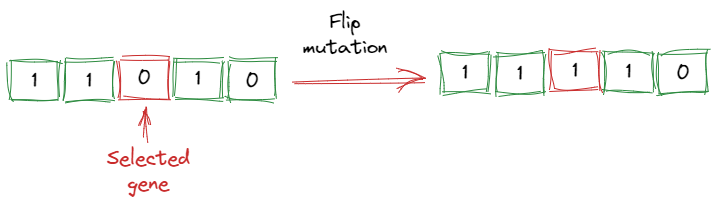
Flip mutation
This type of mutation is performed we use binary crossover. A randomly selected bit of a chromosome is flipped, as shown in the following diagram.
Swap mutation
Such kind of mutation is performed when we encode chromosomes as permutations of a given set of elements. In this type of mutation, the alleles of two randomly selected genes are swapped, as shown in the following diagram.

Random initialization
This is very similar to flip mutation but is used when the chromosome is encoded using discrete values/integers. For example, if a gene's value can be any integer between -5 and 5, we choose a gene at random and reinitialize its value with any integer from the given range. It is also depicted in the following diagram.

Environmental/survivors’ selection
In this phase, it is decided who will survive for the next generation/iteration. Obviously, the survival of good solutions will lead the algorithm to converge while it may cause the algorithm to converge prematurely. Hence, some poor solutions should be given chance to survive, which will allow GA to maintain diversity and enhance exploration. Many selection methods have been proposed in the literature. A few of them are talked about below:
Random selection
In this type of selection scheme, each solution regardless of its fitness will be given an equal chance to survive. Obviously, there will be a chance to lose good solutions.
Proportionate selection
This is exactly the same method that is discussed in the matting section.
Merging parents and new offspring
In such a case, parents and new offspring are merged to make the next generation. Usually, the number of offspring is decided by subtracting the matting pool size from the total population size.
Termination of the algorithm
The termination criteria can be defined in several ways. Three well-known methods are presented below:
A predefined number of iterations are completed.
A predefined fitness value is obtained.
There is no improvement in results for a fixed number of iterations.
Implementation of GA using Python
In this section, we will learn how GA can be implemented in Python to optimize a mathematical function. We will use the same function that we have talked about earlier in this lesson. The mathematical function that we want to maximize is stated below:
The implement of the algorithm is discussed step-by-step in the rest of this section.
xxxxxxxxxxgenes = 2chromosomes = 10lb = -5ub = 5populationSize = (chromosomes, genes)generations = 50mattingPoolSize = 6offspringSize = populationSize - mattingPoolSizeRandom initialization of the population
To randomly initialize the population, we will import numpy library because it offers a function to randomly initialize vectors/arrays.
xxxxxxxxxximport numpypopulation = numpy.random.uniform(lb, ub, populationSize)An example of the random population is printed below where rows show the chromosomes and columns show the genes.
[[ 4.40439216 0.3114284 ]
[-0.42587114 -4.12533052]
[ 0.49616233 -4.68571225]
[-0.88096419 -1.71078592]
[-2.04880589 -3.16450165]
[ 1.73629498 -1.34650208]
[-2.49059838 0.34612405]
[ 1.0395815 4.67268789]
[ 3.44921301 1.21443046]
[ 0.94736171 3.65482178]]
Fitness calculation
The fitness of the whole population can be calculated as follows:
fitness = numpy.sum(population*population, axis=1)
Matting selection
To perform crossover, it is required to first construct the matting pool that will contain the best solutions to take part in the crossover operator. The number of parents will be decided by the mattingPoolSize variable.
1# Following statement will create an empty two dimensional array to store parents
2parents = numpy.empty((mattingPoolSize, population.shape[1]))
3
4# A loop to extract one parent in each iteration
5for p in range(mattingPoolSize):
6 # Finding index of fittest chromosome in the population
7 fittestIndex = numpy.where(fitness == numpy.max(fitness))
8 # Extracting index of fittest chromosome
9 fittestIndex = fittestIndex[0][0]
10 # Copying fittest chromosome into parents array
11 parents[p, :] = population[fittestIndex, :]
12 # Changing fitness of fittest chromosome to avoid reselection of that chromosome
13 fitness[fittestIndex] = -1Crossover
The crossover operator in this section will generate a predefined number of offspring from parents selected in the previous step by using the single-point crossover. In this example, each kth offspring will have the first half from the parent at index (k mod mattingPoolSize) in parents array and second from the parent at index ((k+1) mod mattingPoolSize). It should be noted that there are many other ways to select parents while one of them is implemented here.
1# Following statement will create an empty two dimensional array to store offspring
2offspring = numpy.empty((offspringSize, population.shape[1]))
3
4for k in range(offspringSize):
5 #Determining the crossover point
6 crossoverPoint = numpy.random.randint(0,genes)
7
8 # Index of the first parent.
9 parent1Index = k%parents.shape[0]
10
11 # Index of the second.
12 parent2Index = (k+1)%parents.shape[0]
13
14 # Extracting first half of the offspring
15 offspring[k, 0: crossoverPoint] = parents[parent1Index, 0: crossoverPoint]
16
17 # Extracting second half of the offspring
18 offspring[k, crossoverPoint:] = parents[parent2Index, crossoverPoint:]Mutation
We'll use random initialization mutation because the alleles are continuous values. Each offspring's gene will be chosen at random and initialized to any random value.
Implementation of random initialization mutation.
for index in range(offspring.shape0): randomIndex = numpy.random.randint(1,genes) randomValue = numpy.random.uniform(lb, ub, 1) offspring index, randomIndex = offspring index, randomIndex + randomValue
Environmental selection
In this example, the parents and newly generated offspring will collectively make the next generation. In other words, weak chromosomes in the previous generation will be replaced with new offspring. It is implemented as follows:
Termination criteria
All steps from fitness calculation to environmental selection will be repeated in a loop whereas the total number of iterations will be equal to the variable generations. The complete algorithm is given below:
xxxxxxxxxxprint(bestFitness)import numpy# Parameter initialization genes = 2chromosomes = 10mattingPoolSize = 6offspringSize = chromosomes - mattingPoolSizelb = -5ub = 5populationSize = (chromosomes, genes)generations = 3#Population initializationpopulation = numpy.random.uniform(lb, ub, populationSize)for generation in range(generations): print(("Generation:", generation+1)) fitness = numpy.sum(population*population, axis=1) print("\npopulation") print(population) print("\nfitness calcuation") print(fitness) # Following statement will create an empty two dimensional array to store parents parents = numpy.empty((mattingPoolSize, population.shape[1])) # A loop to extract one parent in each iteration for p in range(mattingPoolSize): # Finding index of fittest chromosome in the population fittestIndex = numpy.where(fitness == numpy.max(fitness))Conclusion
In this lesson, we understood the general structure and working of the Genetic Algorithm. We talked about the source of inspiration behind GA and the different genetic operations used in GA. Moreover, we discussed how GA can be implemented for a continuous optimization function in Python. After reading this lesson, we must be able to implement GA and solve optimization problems using GA.
One Pager Cheat Sheet
A Genetic Algorithm (GA) is a **nature-inspired** algorithm used to solve **optimization problems**, belonging to the branch of **approximation algorithms**, which will be learned in this lesson in terms of its source of inspiration, general structure, working, and implementation.Optimization is the process of finding the best solution to a problem by formulating it mathematically and then using an optimization algorithm such as GA to minimize/maximize the output of a function to reach the optimal solution.- We can use an
optimization algorithmsuch asGAto find the optimal solution of the function . - The process of natural selection is used as an inspiration for
Genetic Algorithm(GA), which generates a population of candidate solutions randomly and selects the fittest individuals to produce similar solutions and ensure the survival of better solutions' traits over time. - GA is a population-based
algorithm, where aset of candidate solutions(chromosomes) are evaluated against anobjective function(fitness function) to find the optimal solution. Genetic Algorithmmimics theprocess of natural selectionwith the use ofgenetic operators, such ascrossover,mutation, andselectionto generate apopulation of random solutionswhich undergofitness evaluationto arrive at the best solution.- A solution is typically encoded as a binary string, integer-valued array, floating-point array, or a
permutationof a fixed set ofelements, depending upon the nature of the problem. - The population is
randomly generatedwithcontinuous variablesin the range of[-5, 5]in order to begin any Genetic Algorithm (GA) or other Evolutionary Algorithm. - The fitness of each of the randomly generated
chromosomesin the population iscalculatedanddepictedin the figure. - The
crossoveroperatoris used to produce new solutions from existing ones in the Genetic Algorithm, and a suitable selection method is necessary to determine theparentsfor the crossover, with two popular methods discussed in the literature. - Selecting the
k bestsolutions from thematting poolis the simplest method for progressing to the next phase of crossover. Fitness Proportionate Selectionis a method of selecting a solution to crossover such that each solution is assigned a probability of selection based on its fitness.- The accumulated probability distribution for this population is calculated by summing the fitness of each solution into the sum of fitness of all previous solutions.
- The crossover operator mimics the sexual reproduction of natural selection and
exchanges genetic informationbetween twoparentsto create newoffspring, with various methods discussed in the literature. - One-point crossover randomly chooses one crossover point and creates two children using the first half of one parent and the second half of the other parent.
Multipoint crossovercreates offspring by selecting alternative portions from both parents at multiple crossover points.- In uniform crossover, each gene for an offspring is chosen with
equal probabilityfrom both Parents,resulting in the exchanged gene positionsin the resulting offspring. - Mutation is a
biological operatorthat introduces new traits in genetic information and helps maintain diversity to prevent populations from converging prematurely. Flip mutationis a type of mutation used with binary crossover, in which a randomly selected bit of the chromosome is flipped.Swap mutationis a kind of mutation where two randomly selected genes have their alleles swapped.- Random initialization is used to re-initialize the discrete values/integers of a gene with a random value from a given range.
- Selection methods are used to decide which solutions will continue into the next generation, such as
random selectionandproportionate selectionwhich gives better solutions a higher chance of surviving, ormerging parents and new offspring, which gives the new generation a mix of both. - The algorithm terminates when
a predefined number of iterations,fitness value, orlack of improvementhas been achieved. - Using the mathematical function , Genetic Algorithm (GA) was
implementedin Python tooptimizethe function. - The population can be randomly initialized using
numpy's function for creating random vectors/arrays. - An example of the
random populationis printed below whererowsshow thechromosomesandcolumnsshow thegenes. - The overall fitness of the
populationis determined by summing up the individualfitness scores. - Making a
matting poolof the best solutions according to the mattingPoolSize variable is essential for successful crossover. Crossoveris used to generate a predefined number of offspring from selected parents, implementing a single-point method to assign each parent's genes to the corresponding offspring.- Mutation, with
random initialization, is used to randomly initialize each offspring's allele to anycontinuous value. - Natural selection occurs through environmental selection, in which
weak chromosomesare replaced with newoffspringfrom the previous generation. - The algorithm of the fitness calculations and environmental selection will be repeated in a loop a total of
generationsiterations. - By understanding the source of inspiration behind and the operations used in Genetic Algorithms, readers should be able to implement and solve optimization problems with GA in Python.


