A Recursive Expression for Weighted Interval Scheduling

As mentioned before, dynamic programming combines the solutions of overlapping sub-problems. Such a problem, the interval scheduling for collecting maximum weights, is relatively easy.

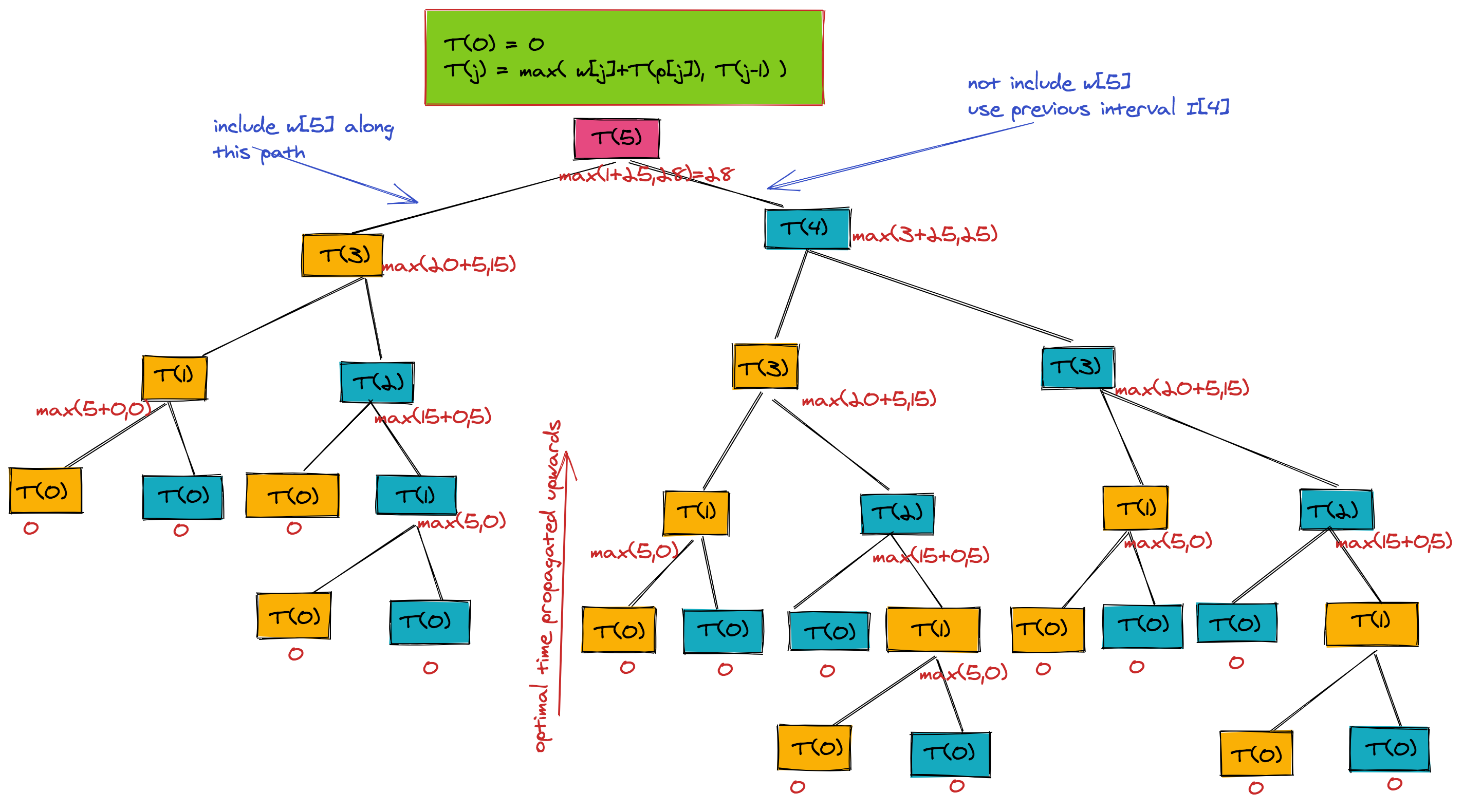
For any interval j, the maximum weight can be computed by either including it or excluding it. If we include it, then we can compute the sum of weights for p[j], as p[j] is the first non-overlapping interval that finishes before I[j]. If we exclude it, then we can start looking at intervals j-1 and lower. The attached is the recursive mathematical formulation.

The below figure shows the recursion tree when T(5) is run.

1Routine: T(j)
2Input: s, f and w arrays (indices 0..n).  Intervals are sorted according to finish times
3Output: Maximum accumulated weight of non-overlapping intervals
4
5Base case:
61. if j==0 return 0
7
8Recursive case T(j):
91. T1 = w[j] + T(p[j])
102. T2 = T(j-1)
113. return max(T1,T2)

xxxxxxxxxx

// Routine: T(j)

// Input: s, f and w arrays (indices 0..n). Intervals are sorted according to finish times

// Output: Maximum accumulated weight of non-overlapping intervals

​

// Base case:

if (j === 0) return 0;

​

// Recursive case T(j):

let T1 = w[j] + T(p[j]);

let T2 = T(j - 1);

return Math.max(T1, T2);