Memoization of Fibonacci Numbers: From Exponential Time Complexity to Linear Time Complexity

To speed things up, let's look at the structure of the problem. f(n) is computed from f(n-1) and f(n-2). As such, we only need to store the intermediate result of the function computed for the previous two numbers. The pseudo-code to achieve this is provided here.

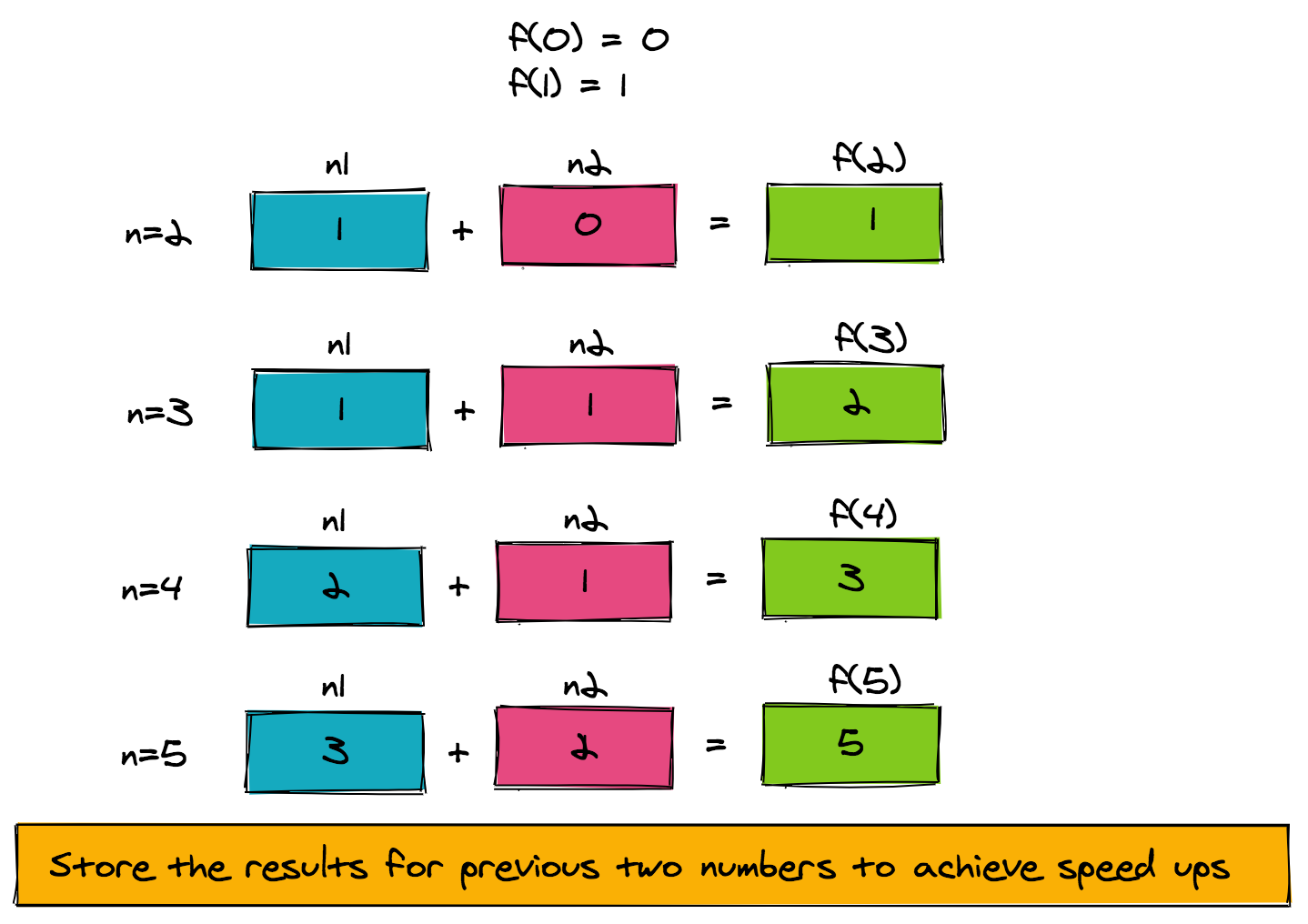
The figure below shows how the pseudo-code is working for f(5). Notice how a very simple memoization technique that uses two extra memory slots has reduced our time complexity from exponential to linear (O(n)).

1Routine: fibonacciFast
2Input: n
3Output: Fibonacci number at the nth place
4Intermediate storage: n1, n2 to store f(n-1) and f(n-2) respectively
5
61. if (n==0) return 0
72. if (n==1) return 1
83. n1 = 1
94. n2 = 0
105. for 2 .. n
11    a. result = n1+n2           // gives f(n)
12    b.   n2 = n1                // set up f(n-2) for next number
13    c.   n1 = result            // set up f(n-1) for next number
146. return result

xxxxxxxxxx

function fibonacciFast(n) {

    if (n === 0) return 0;

    if (n === 1) return 1;

    let n1 = 1;

    let n2 = 0;

    let result = 0;

​

    for (let i = 2; i <= n; i++){

        result = n1 + n2;     // gives f(n)

        n2 = n1;              // set up f(n-2) for next number

        n1 = result;          // set up f(n-1) for next number 

    }

    return result;

}

console.log(fibonacciFast(10));