Weighted Interval Scheduling via Dynamic Programming and Memoization
Our last example in exploring the use of memoization and dynamic programming is the weighted interval scheduling problem.
We are given n intervals, each having a start and finish time, and a weight associated with them. Some sets of intervals overlap and some sets do not. The goal is to find a set of non-overlapping intervals to maximize the total weight of the selected intervals. This is a very interesting problem in computer science, as it is used in scheduling CPU tasks, and in manufacturing units to maximize profits and minimize costs.
Problem Parameters
The following are the parameters of the problem:
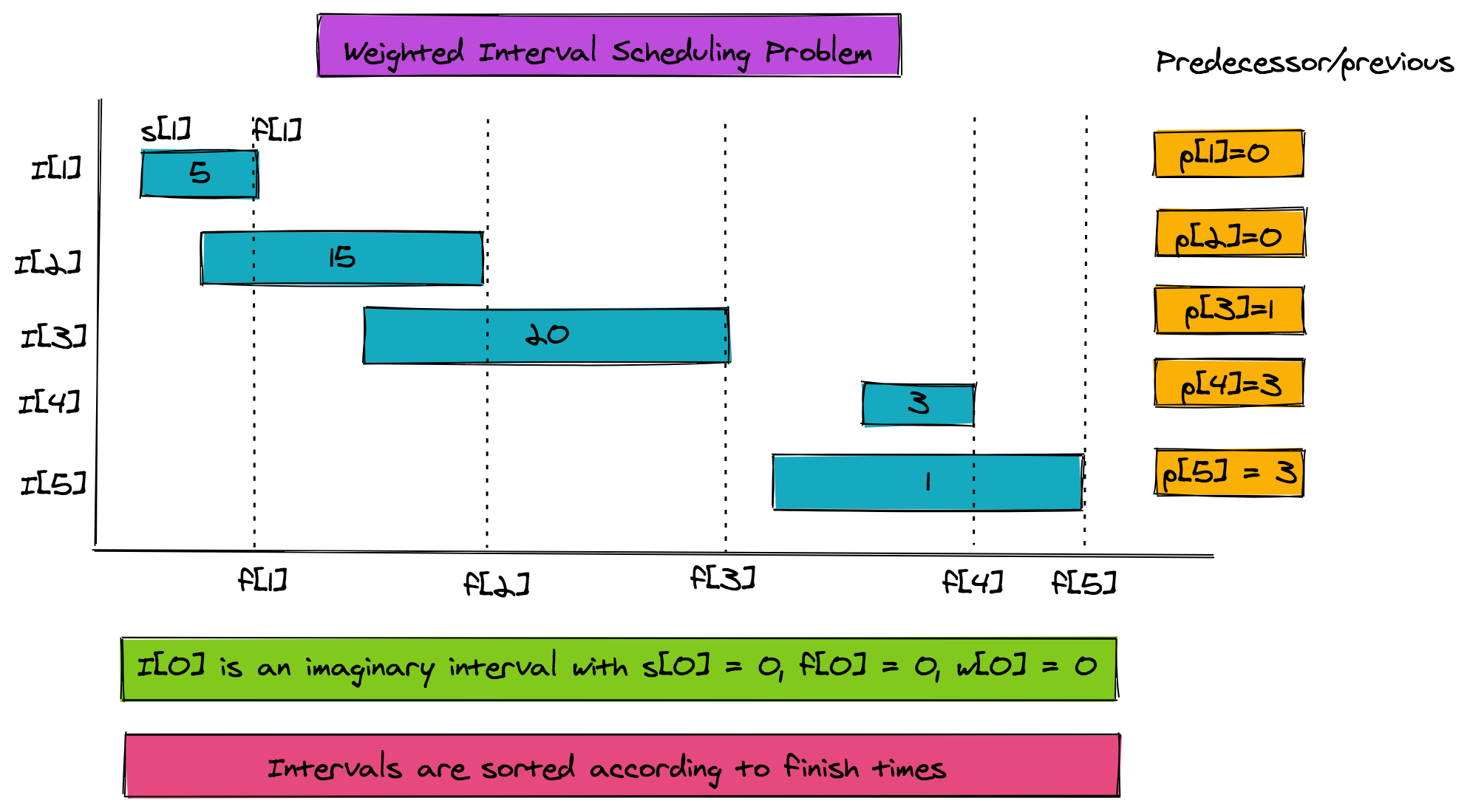
11. n = total intervals. We'll use an additional zeroth interval for base case.
22. Each interval has a start time and a finish time.
3 Hence there are two arrays s and f, both of size (n+1)
4 s[j] < f[j] for j=1..n and s[0] = f[0] = 0
53. Each interval has a weight w, so we have a weight array w. w[j] >0 for j=1..n and w[0]=0
64. The interval array is sorted according to finish times.Additionally we need a predecessor array p:
16. p[j] = The non-overlapping interval with highest finish time which is less than f[j].
2 p[j] is the interval that finishes before p[j]To find p[j], we only look to the left for the first non-overlapping interval. The figure below shows all the problem parameters.