Here is the recursive pseudo-code that finds the maximum reward from the start to the goal cell. The pseudo-code finds the maximum possible reward when moving up or right on an m x n grid. Let's assume that the start cell is (0, 0) and the goal cell is (m-1, n-1).
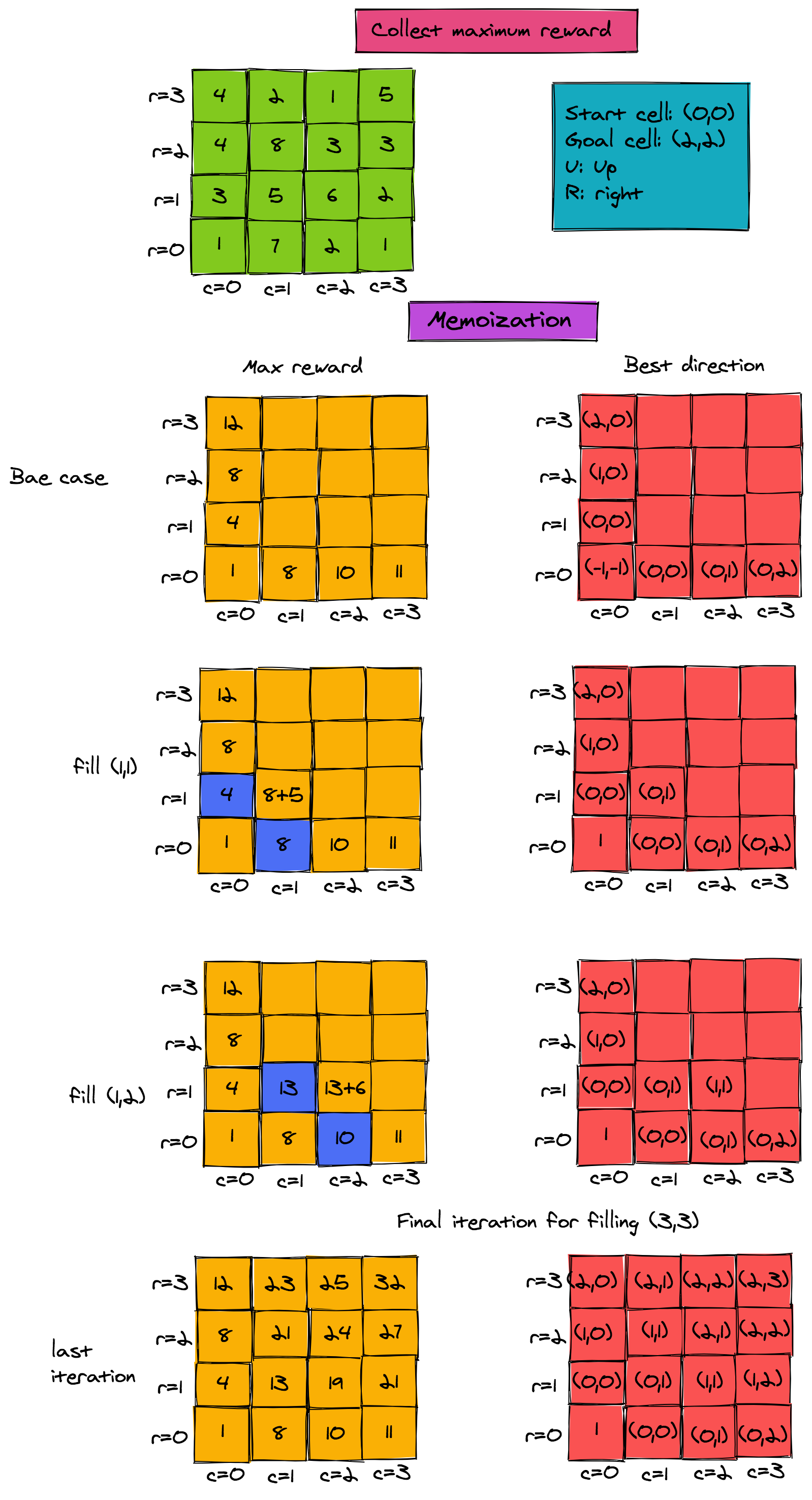
To get an understanding of the working of this algorithm, look at the figure below. It shows the maximum possible reward that can be collected when moving from start cell to any cell. For now, ignore the direction matrix in red.
TEXT
1Routine: maximizeReward
2Start cell coordinates: (0, 0)
3Goal cell coordinates: (m-1, n-1)
4Input: Reward matrix w of dimensions mxn
5
6Base case 1:
7// for cell[0, 0]
8reward[0, 0] = w[0, 0]
9
10Base case 2:
11// zeroth col. Can only move up
12reward[r, 0] = reward[r-1, 0] + w[r, 0] for r=1..m-1
13
14Base case 3:
15// zeroth row. Can only move right
16reward[0,c] = reward[0, c-1] + w[0, c] for c=1..n-1
17
18Recursive case:
191. for r=1..m-1
20 a. for c=1..n-1
21 i. reward[r,c] = max(reward[r-1, c],reward[r, c-1]) + w[r, c]
222. return reward[m-1, n-1] // maximum reward at goal state