Finding the Interval Set

There is one thing left to do-- find out which intervals make up the optimal set. We can use an additional array X, which is a Boolean array. X[j] indicates whether we included or excluded the interval j, when computing the max. We can fill up array X as we fill up array M. Let's change TFast to a new function TFastX to do just that.

We can retrieve the interval set using the predecessor array p and the X array. Below is the pseudo-code:

1let j = n;
2while (j > 0) {
3    if (X[j] === 1) { //Is j to be included?
4        console.log(j);
5        j = p[j]; //get predecessor of j
6    } else {
7        j = j - 1;
8    }
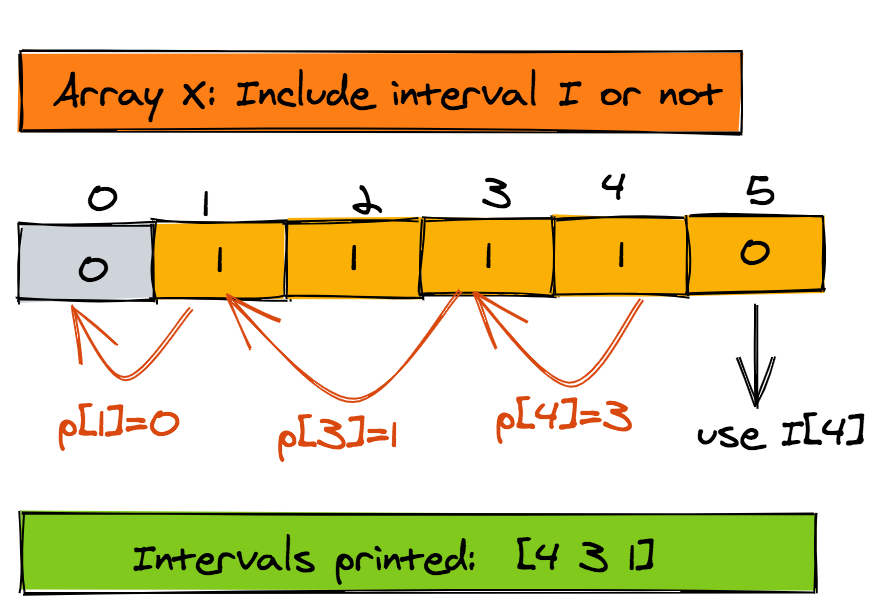
9}

The whole process is illustrated nicely in the figure below. Note in this case too, the intervals are printed in descending order according to their finish times. If you want them printed in reverse, then use a stack like we did in the grid navigation problem. That change should be trivial to make.

1Routine: TFastX(j)
2Input: f,s and w arrays (indices 0..n).  Intervals sorted according to finish times
3Output: Maximum accumulated weight of non-overlapping intervals
4Intermediate storage: Array M size (n+1) initialized to -1,
5                      Array X size (n+1) initialized to 0
6
7Base case:
81. if j==0 
9M[0] = 0;
10X[0] = 0
11return 0
12
13Recursive case TfastX(j):
141. if M[j] != -1            // if result is stored
15return M[j]                 // return the stored result
161. T1 = w[j] + TFast[p[j]]
172. T2 = TFast[j-1]
183. if (T1 > T2)
19        X[j] = 1                    // include jth interval else X[j] remains 0
204. M[j] = max(T1, T2)
215. return M[j]

xxxxxxxxxx

// Javascript Implementation

function TFastX(j, w, p, M, X) { 

  if (j === 0) {

    M[0] = 0;

    X[0] = 0;

    return 0;

  }

  if (M[j] !== -1) {

    return M[j]; 

  }

​

  let T1 = w[j] + TFastX(p[j], w, p, M, X);

  let T2 = TFastX(j-1, w, p, M, X);

  if (T1 > T2) {

    X[j] = 1;

  }

​

  M[j] = Math.max(T1, T2);

  return M[j];

}