Analyzing the Recursion Tree: Uncovering the Achilles' Heel

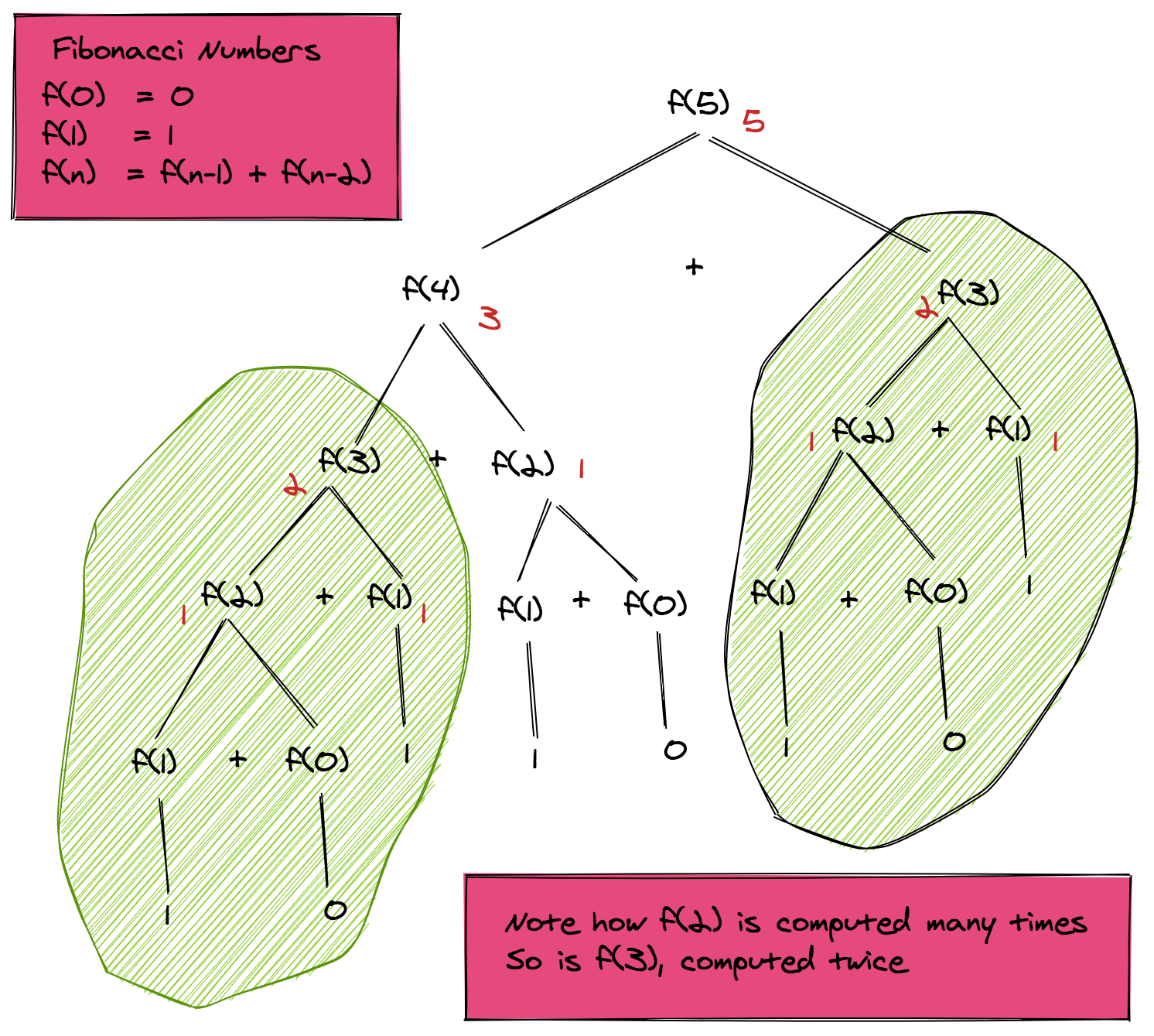
You've seen how the Fibonacci sequence works; now let's peek under the hood. Imagine the Fibonacci sequence as a sprawling tree, where each branch splits into smaller branches until you reach the leaves, which are the base cases.

The Problem of Redundancy

If you study the recursion tree for calculating $f\left(5\right)$, you'll notice something disconcerting. Multiple nodes represent the same Fibonacci number! For example, $f\left(3\right)$ is computed twice, $f\left(2\right)$ is calculated thrice, and the base cases $f\left(1\right)$ and $f\left(0\right)$ appear even more frequently.

Time Complexity: It's Exponential!

Because of this redundancy, our naive recursive approach has a time complexity of $O\left(2^n\right)$. In non-mathematical terms, that means it's slow, especially for larger values of $n$.

The Power of Memoization

Here's the good news: we don't have to live with this inefficiency. By storing the results of computations we've already done, we can avoid redundant calculations. This technique is called memoization, and it's a cornerstone of dynamic programming.

The Road to Optimization

Memoization is like a cheat sheet for your algorithm. It's a simple yet powerful way to remember past results, so you don't have to recalculate them. Here's how it generally works:

Steps to Implement Memoization

1. Create a data structure (usually an array or hash table) to store computed values.
2. Before diving into the recursive calls, check if the result for the current $n$ is already in the storage.
3. If it is, use that value instead of making a new recursive call.
4. If not, proceed with the recursion and store the new result in the data structure.

By doing this, you can dramatically reduce the time complexity from exponential to linear, i.e., $O\left(n\right)$.