Scheduling via Dynamic Programming and Memoization

From the recursion tree, we can see that the pseudo-code for running the T function has an exponential time complexity of O(2${}^n$). From the tree, we can see how to optimize our code. There are parameter values for which T is computed more than once-- examples being T(2), T(3), etc. We can make it more efficient by storing all intermediate results and using those results when needed, rather than computing them again and again. Here's the faster version of the pseudo-code, while using an additional array M for memoization of maximum weights up to nth interval.

1// Routine: TFast(j)
2// Input: f, s and w arrays (indices 0..n). Intervals sorted according to finish times
3// Output: Maximum accumulated weight of non-overlapping intervals
4// Intermediate storage: Array M size (n+1) initialized to -1
5function TFast(j) {
6    // Base case:
7    if (j === 0) {
8        M[0] = 0;
9        return 0;
10    }
11
12    // Recursive case:
13    if (M[j] !== -1) {         // if result is stored
14        return M[j];           // return the stored result
15    }
16
17    let T1 = w[j] + TFast(p[j]);
18    let T2 = TFast(j-1);
19    M[j] = Math.max(T1, T2);
20
21    return M[j];
22}

`

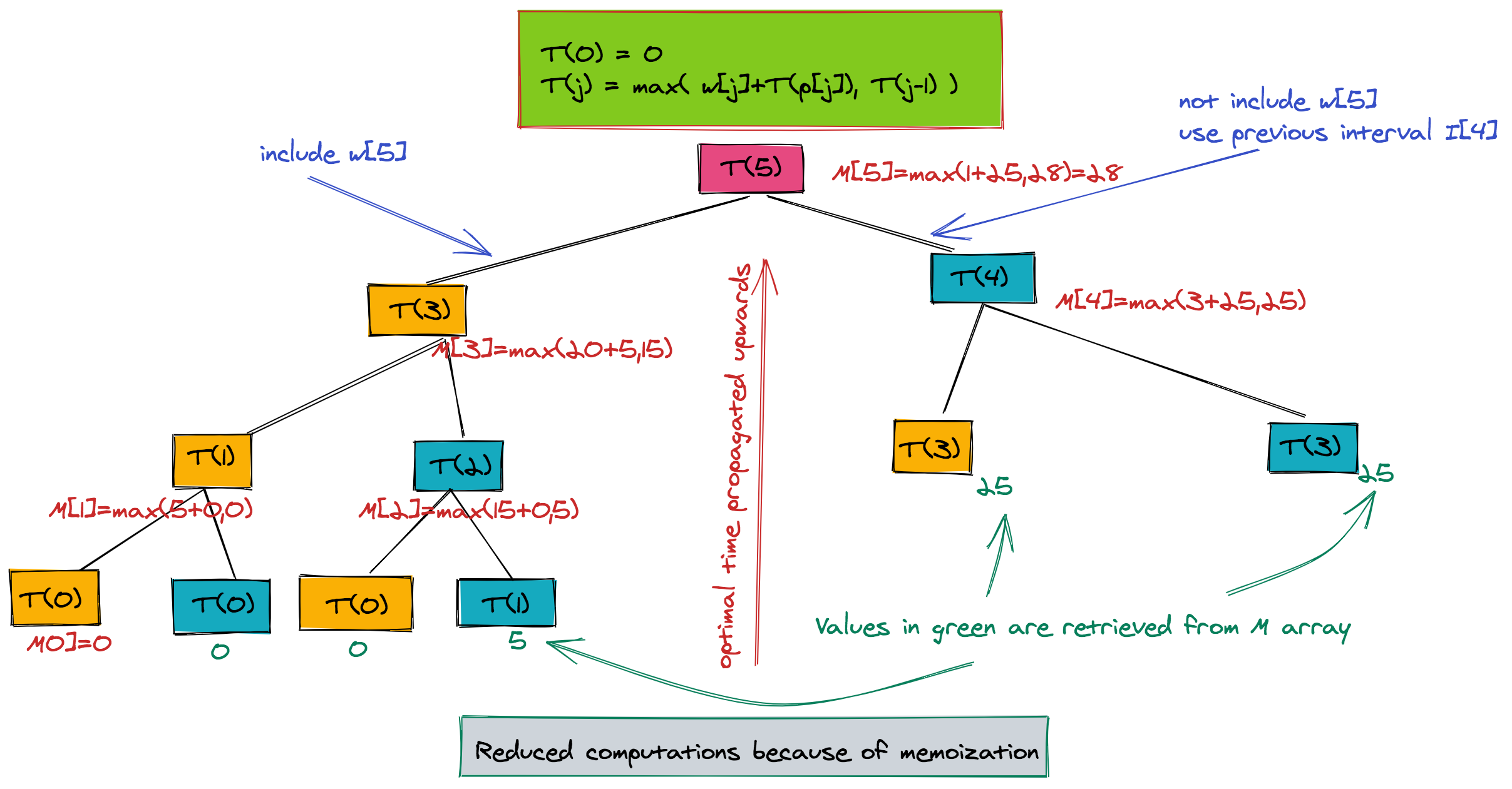
The great thing about this code is that it would only compute TFast for the required values of j. The tree below is the reduced tree when using memoization. The values are still propagated from leaf to root, but there is a drastic reduction in the size of this tree.

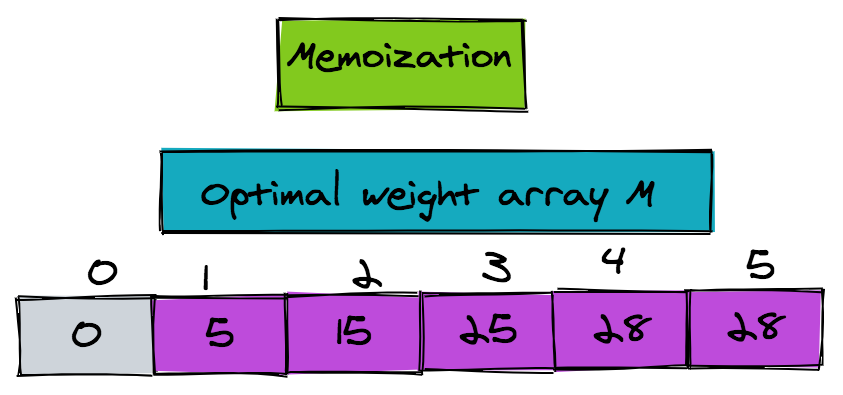
The figure shows the optimal weight array M: